Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae
Red social de Arqueologos e Historiadores
EN BUSCA DEL PLANETA PITAGÓRICO (PARTE PRIMERA)
SOBRE ESTAS LINEAS: Portada del libro: SIMPOSIO SOBRE PATRIMONIO INMATERIAL LA VOZ Y LA IMPROVISACIÓN Imaginación y recursos en la tradición hispánica. Publicado por la Fundación Joaquín Díaz (Urueña -Valladolid 2007-) en el que se recoge mi trabajo sobre temperamentos y astronomía pitagórica. Resumen de la conferencia dada por mí, bajo el título: “Creación, temperación e improvisación” (páginas de la 34 a la 94); donde expliqué la posible relación entre la Armonía Mundi y los secretos de la “improvisación”. Técnicas ligadas a un inconsciente que nos permiten repentizar y crear música de modo inmediato, tan solo guiados por un “sexto sentido” armónico. Intuición que no necesita de unos conocimientos previos o de estudios preliminares de armonía; sino que se produce conforme nos marcaría un instinto. Por lo que aquella improvisación quizás nazca de una armonía preestablecida en los seres humanos, quienes actuarían de un modo semejante al de las aves; capaces de crear belleza con su canto (con el fin de atraer a los de su especie o para alegrar sus vidas). Todo ello relacionado con unos fines de procreación y de “lucimiento” que evidentemente se atiene a unos cánones de belleza natural.
De tal modo existiría una “Belleza Natural” establecida donde las personas estarían dotadas de un instinto animal que comprendería unos cánones de armonía primarios. Aunque a su vez, gozaríamos de una capacidad intelectual que nos permitiría entender que aquella “belleza Natural” se compone conforme a unas reglas cósmicas o universales. En base a unos cánones intelectuales y otros primarios, siendo esos segundos los que igualmente rigen algunas especies del mundo animal; donde -por ejemplo- las hembras eligen al macho que mejor canta, al que tiene un plumaje llamativo, o al que más espectacularmente se mueve en un ritual del cortejo. Ello frente a otros modos de procreación animal que no se basan en la belleza ni en la inteligencia, donde las futuras madres tan solo pueden esperar aparearse con aquellos que son los más fuertes o los que luchan mejor. Otro modo de disputarse la creación (procreación), aunque en este caso por un medio agresivo; en el que las hembras no eligen y los machos “a” suelen tener un rebaño de estas, a las que cubren y guardan hasta que otro semental le destrona.
Consecuentemente y habiendo observado como en el reino animal existen estos dos procesos de selección: Uno, eligiendo a los fuertes -con el fin de evolucionar hacia generaciones menos desvalidas-; y otro, en el que se escogen progenitores más bellos, más inteligentes o con mayor capacidad (para el canto, la danza, etc.; en cortejos fundamentalmente regidos por el aspecto, la inteligencia y la beldad). Podemos concluir que estas reglas de belleza son innatas en la Naturaleza y en gran parte de los seres vivos; en especial entre los humanos. Aunque el hombre ha creado medios de sublimación o comprensión de aquel sentido de la belleza, a través de la ciencia y el arte. Llegando a comprender que ese instinto sobrenatural de atracción hacia lo bello no solo une al reino animal, sino asimismo se contendría en las proporciones matemáticas del arte y hasta en la Armonía del Cosmos (tal como veremos). Siendo estos los principios que regían el concepto antiguo por el cual belleza era sinónimo de divinidad.
BAJO ESTE PÁRRAFO: Dibujo mío (tomado desde el Libro de los Muertos de Ani) en el que vemos “El juicio de Osiris” ; la última sentencia que los dioses egipcios dictaban sobre el alma del difunto -confirmando su salvación o su condena en el más allá-. En la imagen, el fallecido -a nuestra izquierda- espera veredicto, mientras pesan su corazón en la balanza. Anubis actúa como maestro de ceremonia, regulando el peso, mientras diversos dioses juzgan al muerto, o bien le custodian. El resultado del veredicto será positivo si el corazón del que se somete a juicio pesa menos que una pluma de Maat (la diosa de la proporción, de la belleza y la medida). De ello veremos siempre en los juicios de Osiris, un platillo conteniendo el vaso canope que guarda esta víscera del difunto y en el opuesto, aquella pluma de la divina Maat (de avestruz).
El significado de este ritual es tan complejo que en sí mismo desvela gran parte de la filosofía y de la religión egipcia. Pues alude no solo a la bondad de corazón del que es examinado por los dioses, sino también a su actuación conforme a los patrones de pesos y medidas (sin haberlos alterado) o al equilibrio de sus decisiones en vida. Todo lo que quizás pudiéramos comprender si asimilamos este proceso al difunto faraónico, con el Juicio Final que promulga la religión cristiana. Una idea a través de la que nos será fácil comprender como la iconografía de aquella sala de Osiris, se corresponde también con nuestra simbología y forma de ver la justicia, las leyes o la equidad; comúnmente representadas por una dama que sostiene una balanza. Todo ello, en el Mundo Antiguo (en Egipto, Mesopotamia y hasta en Grecia) a su vez se unía a conceptos universales de equilibrio y armonía; que se suponía, eran los que regían el Orbe Cósmico y la Creación. Un Universo que se creía nacido de la perfección del número y de la medida exacta; que unidos, generaban las sensaciones de belleza, procedentes de aquella combinación de las proporciones y numeraciones divinas (tal como el músico era capaz de hacer con su arpa, o el escultor con la piedra).
Regulando estos principios armónicos del Creador, los ciclos siderales, las distancias de los planetas, el tamaño de los astros, junto al tiempo o las formas del Espacio. Un Cosmos en el que el Tiempo era una sucesión de Espacios, mientras aquellas dos categorías (tiempo y espacio) se unían gracias a los mismos principios de belleza y bondad existentes en la Naturaleza. Fuerzas que -como el atractivo sexual o intelectual- hacían armónicamente perfecta y divinamente sublime a la Creación. Siendo este el fin de la búsqueda que el hombre debería realizar durante su vida. Intentando a través del arte, de la creatividad, de sus obras o de su bondad; comprender el espíritu de la armonía divina (todo lo que los egipcios encarnaban en la diosa Maat, la bella de la pluma en el tocado).
A) Los principios del Maat:
Comúnmente se considera que los dioses de Egipto encarnaban un panteismo de tipo primario, olvidando que en verdad esconden una complejísima filosofía cargada de Historia. Para comprender la simplicidad generalizada con la que se explican las deidades y los cultos faraónicos, bastará leer cómo se entienden los edificios o monumentos donde estos eran adorados. Tal como en ocasiones tratan a las Pirámides, comúnmente consideradas simples cenotafios realizados por reyes con un espíritu dictatorial y realizados con el deseo megalómano de imponerse (para dejar su huella sobre el tiempo). Pese a todo, aún hay muy pocos que puedan explicar siquiera cómo pudieron hacerse en plena Edad del Bronce (sin utilizar Hierro, ni menos acero); aunque ciertamente ya hay miles de investigadores que desde mediados del siglo XX se dedicaron a estudiar el verdadero significado de aquellas Pirámides. Encontrando centenares de misterios, algunos irresolubles, entre los que destaca su uso como observatorios astronómicos y como edificios públicos -de gran utilidad científica y social- (1).
Algo semejante suele hacerse al hablar del significado de las deidades del Nilo, considerándolas simples adoraciones cercanas al chamanismo o a la magia de la época, sin reparar en el verdadero valor filosófico y social que contenían. Entre aquellas divinidades incomprendidas del Nilo destacarían casos como el de Maat, la preciosa diosa de la belleza, la armonía y la equidad egipcia; que era representada como una mujer semidesnuda y con una pluma en su frente (aunque a veces aparece como Isis, con alas bajo sus brazos). Dama cuyas facultades se asemejarían a nuestra alegoría de la “Justicia”, pero que en su caso no lucía una balanza en la mano, sino portaba la famosa pluma cuyo peso macaba la salvación del alma del difunto. Atributo sobre el cual hablaremos más tarde, aunque para la comprensión de la dificultad que entraña el concepto de Maat añadiremos que el jeroglífico de “pluma” se leía con voz igual al de la diosa (“maa”); significando esa palabra en Egipto “la verdad” (además de esta parte del ave). Todo lo que expresa que cuando el corazón del fallecido era más ligero o puro que “la verdad”, su alma ascendía a los cielos; tal como realizaban las aves emplumadas -o la misma diosa, que fue también representada con alas tras el periodo de Akhenatón-.
Pese a todo, la idea de Maat se unía asimismo con el principio de “la medida” o “la proporción” divina. Por cuanto a su vez simbolizaba no solo la justicia, sino también el orden cósmico, la paz, la estabilidad y la proporción en la medida o el número. Ideas que los egipcios sublimaban en la belleza de una mujer joven, de proporciones perfectas; señalando claramente de dónde procedía el instinto creador natural, movido por la belleza suprema (siendo obvio que es la mujer el ejemplo máximo de aquella). Una idea que no cuesta entender al contemplar las figuras de las Maat egipcias representadas como féminas preciosas, tocadas con su pluma y muy poco cubiertas. Algo que completa su iconografía propuesta por Akhenatón que la hizo figurar como una mujer alada, enseñando el torso y en actitud semejante al de una bailarina (abriendo los brazos y extendiendo sus alas; todo lo que hace suponer que la figura pudo ser tomada de las bellas danzarinas del Nilo). Sea como fuere, era esta la patrona de los cánones de beldad, pero también de los jueces del faraón (tal como la “dama de la justicia” lo es de los juzgados modernos). Algo que nos enseña que el principio de la estética en Egipto estaba unido al de la ética y regido por en el orden divino, donde Maat acompañaba al dios Thot, encargado de mantener la paz, a estabilidad y de sentenciar a los muertos.
Por su parte, el jeroglífico de “pluma” que dijimos solía leerse como “maa”, tenía un segundo sentido: Esa otra interpretación fue “shu”, cuyo significado era “el vacío” y se relacionaba con un dios de igual nombre. Deidad masculina que se representaba de manera muy semejante a Maat y simbolizaba la luz con el aire, relacionado con los fenómenos celestes. Considerándolo la mitología faraónica como el hermano de la diosa e hijos del gran “Sol”; ambos gemelos estaban presentes en el tribunal del Osiris, en el que Shu solía realizar funciones de acusación. Tal como Susana Alegre nos dice en su magnífico artículo “La pluma de Maat” (2) ; explicando cómo durante las ceremonias funerarias, la “iconografía de Maat y de su pluma son escenas de psicostasia. En este juicio supremo ante el tribunal presidido por Osiris, el difunto debía demostrar su absoluta pureza para poder acceder a la eternidad (…) . Una balanza en perfecto equilibrio era el resultado deseado para acceder a una existencia sin límite (…) el mágico juicio de la psicostasia era realmente duro. Es decir, que el peso más ínfimo era capaz de impedir que el corazón (la conciencia) mantuviera el equilibrio con el casi impalpable símbolo de Maat. Nuevamente la noción de ligereza en su máximo grado parece clave para comprender la simbología expresada por la pluma y su vinculación con Maat” .
IMAGEN ARRIBA: Grabado francés del siglo XVIII de Gravelot y Cochin en el que vemos representada La Justicia, con su sable y su balanza (aunque normalmente también suele ir vendada). Esta dama de los tribunales, cuya alegoría es tan semejante a la de La Ley -que igualmente suele figurarse como una mujer sosteniendo una pesa-; desciende directamente de la Maat egipcia. Aunque en el caso de la diosa antigua sus funciones no se limitaban tan solo al patronazgo de jueces y lugares en que los egipcios administraban sus normas. Sino que además regía los cánones artísticos y los principios de belleza, a la vez que presidía el juicio final ante Osiris; prestando o donando su pluma, para medir con ella el equilibrio de la salvación. Todo lo que nos enseñaría una moral basada en el bien, pero que además admitía el sexo y la admiración hacia el cuerpo humano, como forma natural de lo más divino.
IMAGEN ABAJO: Pequeña esculturita en bronce representando una Maat del Bajo Imperio (entre el 1085 y el 712 a.C.); propiedad del Museo del Louvre, al que agradecemos nos permita divulgar su imagen. A continuación estudiaremos el significado filosófico y científico que pudo tener el concepto de equilibrio en esta diosa que presidía el juicio de los muertos a la vez que los patrones de beldad.
B) La medida y “el Maat”:
.
Muy fácil nos será comprender que el canon de perfección física, unía los conceptos de belleza con unas medidas concretas, lo que llevaba a obtener unos principios generales, basados y comprobados con la ciencia. Hechos que eran fáciles de explicar por medio de las matemáticas, marcando unas proporciones relativas a unas medidas consideradas como perfectas (en el cuerpo del hombre o la mujer). Aunque aquellas proporciones, pasaban a relacionarse con cifras fundamentales (como p , f , o las raíces de 2, 10 etc) lo que llevaba a concretar unos principios numéricos. Por cuanto aquello que podía parecernos muy sencillo, se complementaba con conceptos artísticos mezclados con ideas científicas, hasta llegar obtener unos valores filosóficos -derivados del análisis de los cánones de belleza-. Fórmulas que vemos mantenidas hasta El Renacimiento y en la Ilustración, donde aún se representaban estos modelos de patrón humano relacionados con figuras geométricas o números mágicos (como “pi” o “fi”). Un ejemplo de ello es el conocido “Hombre de Vitruvio” que Leonardo pinta dentro de un cuadrado y un círculo, refiriendo la “cuadratura del círculo”. Al igual que su réplica publicada por Robert de Fludd presidiendo la edición de “Utriusque Cosmi”; en cuya página inicial contiene el grabado de un hombre vitrubiano, rodeado del Universo y simbolizando el macrocosmos.
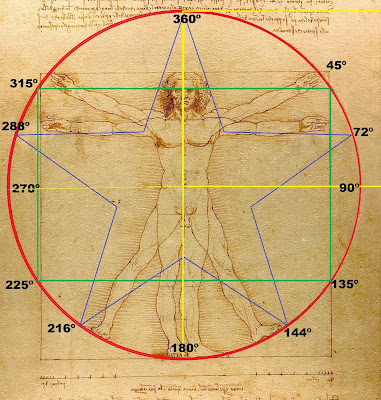
Evidentemente, estas figuras no son el producto de la fantasía, ni menos de la simple imaginación de algunos autores. Sino suponen la representación de la ciencia mística más antigua, que veía al hombre nacido a imagen y semejanza de Dios; concibiendo a su vez un Cosmos surgido del pensamiento y medidas del Creador. Tanto es así, que se relacionaban las proporciones del ser humano con las de los planetas, a la vez que se daba una explicación místico-matemática a estos cánones y tamaños del cuerpo. De ello, la representación del hombre de Vitubrio, en la que el personaje dibujado por da Vinci con los brazos en cruz, a la vez se presenta abriendo piernas y brazos; marcando el tamaño del cuadrado y el círculo entorno a él. Todo lo cual supone que aquellas extremidades humanas marcarían en los dos casos diferentes puntos de la circunferencia:
-Mientras está en pié y con los brazos en cruz, señalan sus extremidades cuatro ángulos, que serían el 360º, en la cabeza; 90º en su mano izquierda, 180º en los pies firmes y 270º en la mano derecha. Lo que llevaba a concretar que la división de círculo en cuatro partes (cuadrantes) era la más perfecta y de ello el enorme valor místico de la cruz.
-Por su parte, cuando el personaje se presenta con las extremidades abiertas (en forma de estrella), tenía 72 grados de la circunferencia en cada una de ellas: Grado 360 en la cabeza; 72º en mano izquierda, 144º en el pié izquierdo; 216º en pié derecho y 288º en la mano derecha. Algo que hacía expresar a algunos filósofos -entre ellos los pitagóricos- que el número 5 era la cifra humana. No solo porque cada mano o pié tiene cinco dedos, sino porque además la circunferencia (de 360º) se divide conforme al cuerpo y sus extremidades en cinco partes. Por lo demás, la vida del hombre era también concebida del mismo modo, con un máximo de 72 años, dividida en cinco etapas de catorce años y medio (completando a esa edad la adolescencia, llegando luego a los 29 para culminar la juventud; a los 43 finalizando la madurez, después a los 58 viviendo como persona mayor, para cumplir 14 más de anciano). Al igual que la estrella dentro del círculo (tal como describe este individuo “vitrubiano” con las extremidades abiertas), era la figura perfecta; pues si dividíamos la circunferencia en cinco puntos y trazábamos líneas entre ellos, dibujando esa estrella, toda su geometría estaba regida por el número fi ( F ) (3) .
SOBRE ESTAS LINEAS: Macrocosmos y microcosmos por Robert Fludd en Utriusque cosmi (maioris scilice); del grabado que preside su edición de 1617 dibujado por T. de Bry. Como veremos en el dibujo siguiente de Leonardo, las posibilidades de relacionar esta figura con números y relaciones geométricas es infinita.
ABAJO : El famoso hombre de Vitrubio pintado por Leonardo, en el que se muestran las proporciones perfectas del cuerpo humano. Tal como Wikipedia recoge en la página dedicada a esta figura ( https://es.wikipedia.org/wiki/Hombre_de_Vitruvio ) ; nos dice textualmente que: Son estas las proporciones descritas por Vitruvio en Los Diez libros de Arquitectura (Marco Lucio Vitruvio Polion, Libro III, Capítulo I): El rostro, desde la barbilla hasta la parte más alta de la frente, donde están las raíces del pelo, mide una décima parte de la altura total. // La palma de la mano, desde la muñeca hasta el extremo del dedo medio, mide exactamente lo mismo. // La cabeza, desde la barbilla hasta su coronilla, mide la octava parte de todo el cuerpo. // Desde el esternón hasta las raíces del pelo equivale a una sexta parte de todo el cuerpo. // Desde la parte media del pecho hasta la coronilla, una cuarta parte de todo el cuerpo. // Del mentón hasta la base de la nariz, mide una tercera parte del rostro. // La frente mide igualmente otra tercera parte del rostro. // El pie equivale a un sexto de la altura del cuerpo. // El codo, una cuarta parte de todo el cuerpo.// El pecho equivale igualmente a una cuarta parte de todo el cuerpo. // El ombligo es el punto central natural del cuerpo humano. En efecto, si se coloca un hombre boca arriba, con las manos y los pies estirados, situando el centro del compás en su ombligo y trazando una circunferencia, esta tocaría la punta de ambas manos y los dedos de los pies.
Además, Leonardo corrige algunas proporciones y añade otras: Cuatro dedos hacen una palma. // Cuatro palmas hacen un pie. // Seis palmas hacen un codo. // Cuatro codos hacen un paso. // Veinticuatro palmas hacen a un hombre.Si separas la piernas lo suficiente como para que tu altura disminuya 1/14 y estiras y subes los hombros hasta que los dedos estén al nivel del borde superior de tu cabeza, has de saber que el centro geométrico de tus extremidades separadas estará situado en tu ombligo y que el espacio entre las piernas será un triángulo equilátero. // Desde la parte superior del pecho al nacimiento del pelo será la séptima parte del hombre completo. // Desde los pezones a la parte de arriba de la cabeza será la cuarta parte. // La anchura mayor de los hombros contiene en sí misma la cuarta parte. // Desde el codo a la punta de la mano será la quinta parte. // Desde el codo al ángulo de la axila será la octava parte. // La mano completa será la décima parte. // El comienzo de los genitales marca la mitad del hombre. // El pie es la séptima parte. // Desde la planta del pie hasta debajo de la rodilla será la cuarta parte. // Desde debajo de la rodilla al comienzo de los genitales será la cuarta parte. // La distancia desde la parte inferior de la barbilla a la nariz y desde el nacimiento del pelo a las cejas es, en cada caso, la misma y como la oreja. // Desde el inicio de la rodilla hasta el inicio de la pelvis, será la misma medida del torso. // Desde el centro del pecho hasta la punta de los dedos, será igual a la longitud de toda la pierna.
Evidentemente todo lo antes expuesto nos podrá parecer absurdo, aunque al lector que no crea que contiene un trasfondo de misterio, preguntaríamos por qué el hombre cuenta (suma o resta) con los dedos y por qué tenemos diez de ellos; siendo la base matemática más perfecta la decena. Tras esta pequeña cuestión que en verdad nos dejará pensativos, propondremos la idea de que durante la Antigüedad la medida y el número perfecto, eran tanto o más necesarios que en la Sociedad Moderna. Pues sin servirse de unas fórmulas métricas proporcionadas con el Arco Terrestre les sería imposible orientarse en el mar, guiase en tierra y menos aún atravesar el desierto. Por ello, una vez más explicamos que tanto la Milla romana, como el Estadio ático, eran proporcionales al tamaño del Globo terráqueo. Perímetro de la Tierra que se mide en el mar o en el desierto de manera muy sencilla, bastando colocar mástiles en linea recta de Norte a Sur para estudiar en que momento su sombra máxima cambia en un grado. Algo sencillísimo de establecer en el Nilo, donde se suceden los tramos de cauce en linea recta Norte Sur (durante centenas de kilómetros). Al igual que en el Egeo, donde es posible establecer una perfecta linea entre las islas, que nos proporcionarán una mira muy exacta con el fin de calcular el Grado.
Siendo así, no nos debe de extrañar que todas las medidas usadas por grandes civilizaciones en la Antigüedad, sean patrones geodésicos; tomados después de medir el Arco terrestre (pues era imprescindible tener una medida derivada del perímetro terráqueo para repartir las tierras, o para viajar). Algo que realizarían ya en el cuarto milenio a.C. en el Golfo Perso Arábigo; cuya profundidad durante cientos de kilómetros a veces no supera los dos metros (permitiendo clavar una hilera de mástiles orientadas al Norte y para estudiar las sombras). Todo lo que explica por qué el Codo de Gudea (rey de Lagash), fuera ya prácticamente igual a nuestros 50 ctms. Algo semejante sucedería con el Codo Egipcio impuesto por Himnotep en tiempos de Djoser (hacia el 2750 a.C.). Trás haber realizado las primeras pirámides y pudiendo calcular con toda facilidad el perímetro terrestre -algo imprescindible para poder estudiar los astros y orientarse- (4) . Estableciendo en Saqaara como medida sagrada el Codo Real de unos 52,46 centímetros. Un patrón métrico que no cambia prácticamente en toda la historia de Egipto, y que tan solo en ciertos momentos se atrevieron a reformar (como sucede en tiempos de Akhenatón -donde aumenta hasta los 25,2 centímetros-; aunque durante el Imperio Bajo y a la llegada de los Ptolomeos lo modificaron, por desconocer su significado y su carácter sacro).
Pese a todo, mientras la civilización egipcia estuvo en plenitud, no se modificaron sus patrones de medida o capacidad (durante dos mil años apenas variaron en micras). Por ello en el juicio de Osiris una de las primeras premisas que el difunto debía demostrar era no haber cambiado jamás las proporciones sagradas (las formas de peso o de longitud establecidas). Ello porque sustituir o modificar los patrones podía significar haber engañado en vida, en la venta de mercancías o tierras. Pero sobre todo, porque de cambiar las proporciones sagradas, los puntos de referencia en la observación de astros y el modo de medir las coordenadas terrestres podrían variar; llevando a perderse en el desierto y a no calcular las horas, ni poder estudiar los astros. Para quienes deseen profundizar en este tema recomendamos leer el siguiente artículo nuestro, o bien consultar los que incluimos en nuestra cita anterior (4) .
SOBRE Y BAJO ESTAS LINEAS: Dos dibujos míos tomados desde papiros o frescos egipcios. Arriba vemos el juicio de Osiris, donde el corazón del difunto es valuado para compararlo con la pluma de Maat. Abajo, una pesada de oro tal como la muestra el papiro matemático Rhind. En este se observa como las balanzas debían de ser de gran exactitud debido al tamaño y diseño sofisticado. Por su parte las pesas solían tener formas de animales (sobre todo de toros) habida cuenta que la “pecunia” -los “pecus” o el ganado- era el bien más preciado en la época y en en que se calculaban las riquezas. Tanto que el nombre de “pecado” procede de esta palabra latina (pecus o pecunia); pues la cabeza de res fue el patrón más común durante la Antigüedad. Habida cuenta que se podía comerciar libremente con un valor de estas características, en el que un determinado número de gallinas se correspondían con un ovino y varios de estos, se cambiaban por un bovino o bien un equino. Siendo el buey (o el toro) la cantidad en la que solía tasarse el salario de un mes, en las Sociedades avanzadas del Mediterráneo.
Por su parte, este trueque pasó a valuarse también en metales durante los tiempos más antiguos; lo que necesitó de unas balanzas de enorme precisión; ya que el gramo de oro o de plata costaba mucho más que en nuestros días (debido a que bajaron tras la entrada de estos metales desde América o a la existencia de otros bienes de inversión). La precisión y exactitud en el pesado era tal, que Mesopotamia o Babilonia tenía patrones como “el grano” que se correspondía a 0,045 gramos; siendo su base común el Keratión (de 4 granos) que fue su primer ponderal equivalente a nuestro gramo aunque solo pesara 0,18 grs.. Por su parte, en Egipto la medida oficializada era el Shaty (palabra que pudo originar la voz Siklo) cuyo peso fue de unos 7,5 gramos y que se subdividía en varias fracciones. Estos Shaty se comercializaban comúnmente como anillos de oro de 7,5 g., que veíamos representados en el dibujo bajo estas lineas (aunque con los modelos muy aumentados de tamaño o valor).
Debido a lo que narramos, el mundo de los pesos y de las medidas pertenecía a los científicos más especializados, tal como en nuestro tiempo los más destacados matemáticos también se dedican a la economía y a las finanzas. De ello, el arte de los ponderales y metrología hace miles de años se conservaba y estudiaba con esmero en los templos (que actuaban como juzgados en caso de litigio); por lo que no debe extrañarnos que se mezclase con el estudio de los astros y de los dioses. Llegando a conformar en Mesopotamia y en Egipto unas teorías que estudió y recogió Pitágoras en sus lugares de origen; importándolas posteriormente a la Hélade y Magna Grecia. Desde donde se divulgó el “dogma” que tan secretamente conservaron los templos egipcios o babilónios y que también guardaban mistéricamente los pitagóricos; aunque llegó hasta nuestros días gracias a Platón. Quien compró y “readaptó” los textos de los pitagóricos; divulgando así estos secretos cuya difusión se castigaba con pena capital entre los de Pitágoras (copiando las pautas de conducta sacerdotal del Nilio o de Mesopotamia; donde igualmente desvelar los misterios que guardaba el clero era severamente castigado) (5) .
C) El templo y sus funciones en la balanza:
Tras los conceptos antes presentados, comprenderemos que el orden de pesos y medidas pertenecía al mundo de lo más sacro; pues de su permanencia y exactitud dependía el buen funcionamiento del mercado y de la economía. Ya que al cambiarlos o alterarlos no solo se podía producir el caos interior, sino que además se hacía imposible el comercio exterior (cuyos valores de cambio estaban perfectamente establecidos en sistemas de común valencia -lo que se llamaba coeficiente de paso de un sistema a otro-). Por lo demás, los patrones sagrados de esos pesos y medidas (de capacidad o longitud) igualmente se guardaban en los templos, actuado el sacerdote supremo y el edificio principal, como custodio de esos modelos.
Para corroborarlo bastará leer en el Antiguo Testamento la construcción del Templo de Salomón, en donde se describe qué capacidad contiene cada pila y qué medida tiene casa sala. Todo lo que atestigua que para comprobar el valor del Codo Sagrado judío, la del siklo y la “piscina” hebrea, bastaría con medir la capacidad de sus pilas sagradas o la longitud de las habitaciones del gran templo. Aunque hemos de pensar (como ya dijimos) que en el lugar más sagrado del tabernáculo conservarían aquellos patrones, por si habían de probarlos, en caso de importante litigio. Por todo lo que ya dijimos que -a mi juicio- estos eran los tesoros que escondía en el Arca de la Alianza; donde se narra que guardaban la Vara de Aarón y el Maná (a más de Los Diez Mandamientos). Vara que -como ya comenté en varios de mis estudios- (6) consistiría en el patrón del Codo Judío, medida que a mi entender fue tomada por los israelitas en tiempos de Akhenatón; seguramente cuando “se independizaron” del Nilo. Codo Real que en época de este Amenofs IV había sido reformado y aumentado, llegando al ser un patrón geodésico muy exacto, lo que serviría para estudiar los astros y guiarse en el desierto (tal como se narra hizo Moisés). Por su parte, el Maná a mi entender era la Mina; palabra que en idiomas semitas se pronuncia “mâná” ; para comprobarlo ver la cita (7) ”Tabla de Gudea”-; que hubo de ser el modelo del talento o peso hebreo para metales (ponderal derivado de cubicar el Codo judeo-egipcio de unos 52,5 centímetros). Así pues, la historia del Maná encajaría con a mina o medida de metal mesopotámica, de la que vivirían los judíos antes de establecerse en Israel; seguramente al vagar errantes por el desierto como comerciantes de cobre (pues los lugares que cita el Antiguo Testamento en el Éxodo son muy ricos en minas de ese metal).
Todo lo antes expuesto nos explica qué función tenían los sacerdotes y sus enormes edificios sagrados, donde no solo se custodiaban y veneraban los dioses; sino que además guardaban los patrones y las leyes. Leyes como el Decálogo Mosáico y patrones métricos absolutamente necesarios para que no se produjeran engaños en el mercado. Modelos que los propios fieles podrían comprobar de una manera tan sencilla como midiendo las salas del templo o la capacidad de sus pilas (algo que con seguridad los clérigos dejarían hacer a cualquier persona, a cambio de recibir unos codos de tela o unas ánforas de vino, sobre las cuales quería estudiarse su capacidad o longitud). Por su parte, estos templos también tenían como función la del pesaje y cambio de metales preciosos; una labor fundamental antes de la aparición de la moneda. Siendo la única garantía posible por entonces, que el oro y la plata estuvieran medidos y contrastados por el sacerdocio; debido a ello, en Egipto existía un cuerpo de funcionarios dedicados a este oficio (comúnmente adscritos a una “casa sagrada”). Pues estos pesadores oficiales no solo debían conocer el peso exacto en cada caso, sino asimismo la pureza del metal. Unos kilates que por entonces tan solo se lograban calcular aplicando patrones de peso y volumen; es decir, hundiendo la pieza en agua y estudiando la capacidad de desplazar líquido, conforme a su peso -aunque para ello se precisa de un juego de pesas y vasos perfectamente regulado; tanto como unas reglas graduadas para modelos de oro, plata, estaño y cobre-. A ello hemos de unir la obligación de esta casta funcionarial o sacerdotal por controlar la procedencia del oro y la plata; con el fin de no permitir que ajenos al poder (o al templo) introdujeran metales preciosos sin una regulación establecida (con el fin de que no se devaluase, tanto como para evitar lo procedente de robos).
SOBRE ESTAS LINEAS: Fotografía de un Shaty de oro cercano a tiempos de Akhenatón, cuando esta medida se correspondía con unos 7,5 gramos (debido a que el Codo Real era de 52,5 ctms.; igual al Codo Hebreo). Tal como decimos, la función de pesar los metales y calcular su pureza fue uno de los trabajos más importantes que tuvieron los clérigos y funcionarios de los santuarios (al menos hasta la expansión de la moneda, en el siglo VII a.C.). De ello, no nos extraña el pasaje bíblico en el que Cristo echa a los cambistas y mercaderes del templo, todo lo que significa que no deseaba ya que esta función de valuar y cambiar los metales fuera ya de los sacerdotes. Sino que el Estado y las organizaciones privadas debían dedicase a una labor tan económica como dudosa (pues evidentemente facilitaba que actuasen como bancos o intermediaran ante ellos, en cualquier operación en la que intervenían).
BAJO ESTE PÁRRAFO: La repercusión y el estudio de las matemáticas o la física derivado hacia el arte, procede en principio de algunos “trucos” que los artistas precisan para hacerse con unas técnicas que les permitan crear sus modelos. De ello, es perfectamente comprensible que los arquitectos pretendieran buscar unas medidas perfectas, para que las proporciones de los edificios fueran más bellas. Todo lo que logran en gran parte aplicando los principios de “fi” sobre aquellos; al observar y comprobar que las líneas cortadas bajo este parámetro conforman una proporción perfecta (tanto que es la que actualmente siguen modelos como las cámaras fotográficas o las pantallas de cine -en relación F -). Desde allí, un complejo sistema de comprensión de la belleza unido a cánones y a matemáticas, llevaron a un barroquismo en el que todo parecía tener explicación física o científica (al menos así lo intentaban). Aunque el principio básico de estas teorías procedía en primer lugar para generar técnicas artísticas -sobre todo de perspectiva-. Como la que vemos representada en este grabado de Durero. Donde se observa al pintor, copiando la realidad valiéndose de “trucos y máquinas”, con el fin de lograr una perspectiva perfecta.
Todo cuanto narrábamos anteriormente expresa la necesidad de una gran formación por parte de los sacerdotes cambistas (o funcionarios pesadores), quienes debían conocer hasta el medio de comprobar la pureza de los metales preciosos. Algo que ya supone un alto aprendizaje en la conjugación de los ponderales, medidas y volúmenes. Por su parte, la manutención y explicación de la razón de ser de los patrones métricos igualmente suponía una enorme formación; ya que el templo debía enseñar a los continuadores en sus funciones cómo y por qué habían de conservar las medidas inalterables. No solo por un problema de mercado, sino sobre todo para evitar errores en los estudios y observación de los astros; demostrando a sus alumnos cómo al no modificar las medidas y los parámetros, se podía estudiar el Universo perfectamente desde observatorios antiguos (calculando las horas, los días o los años). Aunque sobre todo debían mantenerse inalterables los patrones, para que los guías de los ejércitos y los pilotos de las caravanas (o de naves) no se perdieran en el mar ni en el desierto.
Evidentemente, de todo ello se desprendería la conclusión de que aquella metrología nacía desde la geodesia. Es decir: Que eran proporcionales al Arco terrestre, el Codo egipcio y el hebreo (de 52,5 ctms), el Codo mesopotámico (de 49,8 ctms); tanto como el babilonio (de 49,5 ctms) o el Estadio ático (de 185 mts). Aunque muy pocos -o casi ninguno- llegarían a dilucidar tal conclusión; pese a que sabían usar aquel patrón perfectamente para guiarse, sin conocer su razón “mágica” de resultados (el por qué les servía para calcular los astros o la situación de coordenadas). Algo común cuando se unen ciencia y religión, donde al final los modelos se mantienen como sagrados durante milenios, llegando a componer un dogma y sin conocerse su fundamento inicial. Pues aunque en nuestros días parece evidente que determinados Codos y Millas servían para guiarse (al ser proporcionales al Arco de la Tierra); hace miles de años tan solo divulgar al pueblo la esfericidad terráquea, podía suponer romper secretos de Estado (o del templo) y por lo tanto “anatema” penado con la muerte. Pues determinados conocimientos tan solo los compartirían algunos, muy capacitados y siempre bajo la vigilancia del poder.
Pese a todo lo que intentaron ocultar, a día de hoy hay evidencias que desvelan cómo conocían determinados hechos, sin los que hubiera sido imposible vivir o guiarse en el desierto. De tal manera y como sabemos que fue Imnhotep el encargado de calcular el valor del Codo, en tiempos de Saqqara. Tras observar que la pirámide de Saqqara está prácticamente sobre el Grado 30º (N) y que este Codo ya tiene una correspondencia bastante exacta con el perímetro de la Tierra. Podemos dilucidar que ya en esta época se calculó el Grado, con bastante exactitud, dado que el Codo Real de Imnhotep medía unos 52,44 centímetros. Así, sabiendo que el Estadio egipcio del que habla Eratóstenes se componía de 300 Codos (unos 157,32 metros en epoca de Inmhotep). Siguiendo el dato que Eratóstenes de Cirene obtuvo en la Biblioteca de Alejandría y que no supo justificar: Si el Perímetro de la Tierra era de 252000 estadios (según escribió éste bibliotecario, aunque sin saber calcularlo debidamente); ello supone que el Arco total que habían estimado en Saqqara fue de 39.644.640 metros (con un error de unos 355 kmts). Del mismo modo, hubieron de estudiar el perímetro terrestere en la Mesopotamia de Gudea; cuando imponen ya un Codo de 49,8 ctms y por lo tanto, casi igual al medio metro (con un error de unos 160 kms). Para finalizar, diremos una vez más que para calcular la circunferencia terrráquea basta con clavar estacas en línea -de Norte a Sur-, a igual distancia, para medir en qué momento su sombra máxima cambia un grado (el mismo día); descubriendo que lo hace aproximadamente a los 111 kilómetros. Por todo cuanto hemos narrado comprenderemos como en el siglo XVIII, la Ilustración (que tanto admiraba las civilizaciones antiguas) copió estos sistemas metrológicos de la Antigüedad. En los que la medida estandarizada se correspondía con el Arco terrestre y las de peso o capacidad, con la cubicación de ese patrón geodésico. Debido a lo que en el siglo XIX se impuso el sistema métrico decimal, donde el metro es la diezmilésima del cuadrante terráqueo y una tonelada, o mil litros, son un metro cúbico de agua -método igual a los modelos metrológicos egipcios, mesopotámicos y grecolatinos- ver (7) .
SOBRE ESTAS LINEAS: De nuevo un fresco egipcio, en el que vemos un funcionario pesando oro (de la Tumba de Menena; Tebas Nº68 -agradecemos a la Institución Valle de los Reyes nos permita divulgar la imagen-). Observemos en el lado contrario la pesa con forma testa de de toro, marcando el valor en cabezas de ganado.
BAJO ESTE PÁRRAFO: Codo Amenofis II; hemos detallado y enmarcado en rojo las medidas que marcaba una imagen de Laura Donatelli (en LA VIDA COTIDIANA DE LOS EGIPCIOS; agradecemos a la autora nos deje tomar como fondo su ilustración). La pieza original está en el Museo Turín, donde podemos ver que la medida del Codo Real es prácticamente 52,5 ctms y la de su Codo Vulgar de 45 ctms (todo lo que se ajusta a principios geodésicos y a conceptos muy cercanos al sistema métrico). Por lo demás, el coeficiente de paso de este Codo hasta el babilonio es tan simple como aplicar 11 (0,45 · 11 = 49,5).
.........................................................................................
CITAS:
(1): Nos gustará en este caso recordar como fue recibido, tan solo hace unos treinta años, el libro de Peter Tompkins “Secretos de la Gran Pirámide” (editado en España hacia 1986 por Javier Vergara). Considerando sus datos como esotéricos o fantásticos, cuando una mayoría de aquellos tan solo referían cómo las Pirámides estaban orientadas de forma astral y construidas a modo de observatorios astronómicos. Mientras no se tuvo muy en cuenta gran parte del relato histórico, en el que Tompkins narraba el modo en que los investigadores de los siglos XVIII y XIX, se sirvieron de estas pirámides para corroborar o realizar sus descubrimientos científicos (relacionados con la medición del Globo Terráqueo o incluso con la gravedad).
Susana Alegre García. Asociación de amigos de la Egiptología. Para los interesados VER:
(3): Acerca de la relación entre la circunferecia con una estrella de cinco puntas trazada en su interior y el número “Fi” bastará señalar que esta cifra que marca la proporción Áurea 1,6180339887498948482045868343656...
es igual a la mitad del Seno de 36; es decir igual a a Cuerda de 72º.
Ello supone que las aspas o lineas de una estrella de cinco puntas trazada en el interior de una circunferencia son iguales a esta cuerda de 72º; es decir el diámetro dividido por 1,61803398874...
Diámetro : “FI” = Cada línea de la estrella de cinco puntas trazadas dentro del Diámetro.
(4): La evidencia de que en la Antiguedad las grandes civilizaciones manejaban patrones geodésicos se manifiesta en que sus medidas son proporcionales a las terrestres. Para comprobar o estudiar cuanto afirmamos recomendamos leer los siguientes artículos nuestros:
- METROLOGÍA EN EL MUNDO ANTIGUO: Sobre ponderales y modelos de logitud; hipótesis peninsulares prerromanas. CONTINUACIÓN (parte tercera). TRATA SOBRE EL SIGNIFICADO DE LA MEDIDA EN LA ANTIGÜEDAD, TANTO COMO DE SUS VALORES. CONSTA DE TRES ARTÍCULOS:
- METROLOGÍA EN EL MUNDO ANTIGUO: Sobre ponderales y modelos de logitud; hipótesis peninsulares prerromanas (parte primera). http://loinvisibleenelarte.blogspot.com.es/2014/05/metrologia-en-el-mundo-antiguo-sobre_3354.html
-METROLOGÍA EN EL MUNDO ANTIGUO: Sobre ponderales y modelos de logitud; hipótesis peninsulares prerromanas. CONTINUACIÓN (parte segunda). http://loinvisibleenelarte.blogspot.com.es/2014/05/metrologia-en-el-mundo-antiguo-sobre_4016.html
3.- METROLOGÍA EN EL MUNDO ANTIGUO: Sobre ponderales y modelos de logitud; hipótesis peninsulares prerromanas. CONTINUACIÓN (parte tercera). http://loinvisibleenelarte.blogspot.com.es/2014/05/metrologia-en-el-mundo-antiguo-sobre_5.html
- CONCLUSIÓN FINAL A LA METROLOGÍA Y PONDERALES; DE LA EDAD DEL BRONCE A LA DEL HIERRO -su pervivencia en época grecorromana y su perduración hasta nuestros días-. Es la conclusión a los tres artículos anteriores. CONTIENE UNAS TABLAS DE CONCORDANCIA que bajo este marcamos. http://loinvisibleenelarte.blogspot.com.es/2014/05/conclusion-final-la-metrologia-y.html
a) Tablas de concordancia del artículo: CONCLUSIÓN FINAL A LA METROLOGÍA Y PONDERALES; DE LA EDAD DEL BRONCE A LA DEL HIERRO -su pervivencia en época grecorromana y su perduración hasta nuestros días-. http://loinvisibleenelarte.blogspot.com.es/2014/05/tablas-de-concordancia-del-articulo.html
- METROLOGÍA Y PONDERALES EN LA IBERIA PRERROMANA (Sobre los estudios de Mora Serrano y de Ma.Paz García-Bellido) http://loinvisibleenelarte.blogspot.com.es/2014/06/metrologia-y-pon...iberia.html
(5): Acerca de la historia del pitagorismo y su permanencia hasta la Edad Media, existe un magnífico trabajo presentado hace unos seis años en la universidad de Salamanca: NUMERUS-PROPORTIO EN EL DE MUSICA DE SAN AGUSTÍN (Libros I y VI) LA TRADICIÓN PITAGÓRICO-PLATÓNICA . Tesis doctoral de Mayo de 2009 ; de GUILLERMO LEÓN CORREA PABÓN. Obra que en posteriores artículos resumiremos y sobre la que merece la pena realizar un buen estudio.
(6): De nuevo y sobre el tema de la Vara de Aarón y el Maná recomendamos leer este artículo nuestro:
1.- METROLOGÍA Y PONDERALES EN EL MUNDO PRE-TARTESSIO http://loinvisibleenelarte.blogspot.com.es/2014/03/metrologia-y-ponderales-en-el-mundo-pre_3546.html
(7): Para mostrar cuanto decimos, a continuación les ofrecemos una tabla correlativa de medidas, realizada por mí.
TABLA DE CONCORDANCIA primera
Medidas egipcias REINO ANTIGUO (2800-2200 a.C.)
LONGITUD
Dedo 18,7 mm.
Palma 4 dedos 74,8 mm.
Spanna 3 palmas 224,4 mm.
Pie 299,2 mm.
Codo Vulgar 2 spanne, 6 palmas 448,8 mm.
Codo real 7 palmas 523,6 mm.
Cadena 100 pies 29,92 mts
Estadio 6 cadenas 179,52 mts.
Pasaranga 30 estadios 5385,6 mts.
Scheno 2 pasarangas 10771,2 mts.
Estadio 300 Codos Reales 157,08 mts.
Pasaranga 30 Estadios Reales. 4712,4 mts.
PESOS
Hekat (líquidos) = Codo Real3/30 = (523,6 al cubo) : 30 = 4,7849 litros
Henu (Hin -ó Hinw-) = Codo Real3/300 = Hekat/10 = 478,49 gramos agua.
Shaty (SHti) peso metal = (Codo Real3/300):64 = 7,4764 gramos -oro, plata etc-
Deben (Dbn) peso metal = Codo Real3/1600 = 12 Shatys = 89,7178 gramos.
LIBRA de 6 Deben = 538,3 gramos
Mina de 50 y 100 Shatys = 373,82 y 747,64 gramos.
ESTIMACIÓN DEL MERIDIANO
75600000 Codo Real de 523,6 mm. = 252000 Estadios de 300 Codos = 39.584.160 kmts.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA segunda
Medidas egipcias REINO MEDIO (2050-1750 a.C.)
Ajustadas a las de Lagash; coeficiente de paso 10/9.
LONGITUD
Dedo 18,694 mm.
Palma 4 dedos 74,77 mm.
Spanna 3 palmas 224,33 mm.
Pie 299,108 mm.
Codo Vulgar 2 spanne, 6 palmas 448,66 mm.
Codo Real 7 palmas 523,44 mm.
Cadena 100 pies 29,9108 mts.
Estadio 6 cadenas 179,4648 mts.
Pasaranga 30 estadios 5383,944 mts.
Scheno 2 pasarangas 10767,888 mts.
Estadio 300 Codos Reales 157,032 mts.
Pasaranga 30 Estadios Reales. 4710,96 mts.
PESOS
Hekat (líquidos) = Codo Real3/30 = (523,443) : 30 = 4,7805 litros
Henu (Hin -ó Hinw-) = Codo Real3/300 = Hekat/10 = 478,05 gramos agua.
Shaty (SHti) peso metal = (Codo Real3/300):64 = 7,469 gramos -oro, plata etc-
Deben (Dbn) peso metal = Codo Real3/1600 = 12 Shatys = 89,63 gramos.
LIBRA de 6 Deben = 537,81 gramos
Mina de 50 y 100 Shatys = 373,45 y 746,9 gramos.
ESTIMACIÓN DEL MERIDIANO
75600000 Codo Real de 523 mm. = 252000 Estadios de 300 Codos = 39.572.064 kmts.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA tercera
Medidas egipcias REINO NUEVO (1580-1085 a.C.)
LONGITUD
Dedo 18,75 mm.
Palma 4 dedos 75 mm.
Spanna 3 palmas 225 mm.
Pie 300 mm.
Codo Vulgar 2 spanne, 6 palmas 450 mm.
Codo Real 7 palmas 525 mm.
Cadena 100 pies 30 mts.
Estadio 6 cadenas 180 mts.
Pasaranga 30 estadios 5400 mts.
Scheno 2 pasarangas 10800 mts.
Estadio 300 Codos Reales 157,5 mts.
Pasaranga 30 Estadios Reales. 4725 mts.
PESOS
Hekat (líquidos) = Codo Real3/30 = (5253) : 30 = 4,8234 litros
Henu (Hin -ó Hinw-) = Codo Real3/300 = Hekat/10 = 482,34 gramos agua.
Shaty (SHti) peso metal = (Codo Real3/300):64 = 7,536 gramos -oro, plata etc-
Deben (Dbn) peso metal = Codo Real3/1600 = 12 Shatys = 90,439 gramos.
LIBRA de 6 Deben = 542,636 gramos
Mina de 50 y 100 Shatys = 376,8 y 753,6 gramos.
ESTIMACIÓN DEL MERIDIANO
75600000 Codo Real de 525 mm. = 252000 Estadios de 300 Codos = 39.690.000.000 mts.
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::.
TABLA DE CONCORDANCIA cuarta
Medidas egipcias Época Baja y Tardía (I milenio a.C.)
LONGITUD
Dedo 18,785 mm.
Palma 4 dedos 75,1428 mm.
Spanna 3 palmas 225,428 mm.
Pie 300,57 mm.
Codo Vulgar 2 spanne, 6 palmas 450,85 mm.
Codo Real 7 palmas 52,6 ctms.
Cadena 100 pies 30,057 mts.
Estadio 6 cadenas 180,342 mts.
Pasaranga 30 estadios 5410,26 mts.
Scheno 2 pasarangas 10820,52 mts.
Estadio 300 Codos Reales 157,8 mts.
Pasaranga 30 Estadios Reales. 4734 mts.
PESOS
Hekat (líquidos) = Codo Real3/30 = (5263) : 30 = 4,8234 litros
Henu (Hin -ó Hinw-) = Codo Real3/300 = Hekat/10 = 482,34 gramos agua.
Shaty (SHti) peso metal = (Codo Real3/300):64 = 7,57976 = 7,58 gramos -oro, plata etc-
Deben (Dbn) peso metal = Codo Real3/1600 = 12 Shatys = 90,96 gramos.
LIBRA de 6 Deben = 545,76 gramos
Mina de 50 y 100 Shatys = 379 y 758 gramos.
ESTIMACIÓN DEL MERIDIANO
75600000 Codo Real de 526 mm. = 252000 Estadios de 300 Codos = 3976560000 kmts.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA quinta
Medidas y pesos de Gudea (siglo XXII a.C).
Longitud
Más pequeña unidad de longitud es el que ella (barleycorn), de alrededor de 1/358,56 metros.
6 se = 1 shu-si (el dedo) 16,6 mm. // 30 shu-si = 1 kush (codo) 498 mm. // 6 kush = 1 gi / qanu (reed) 298,8 ctms. // 12 kush = 1 nindan / GAR (varilla .) 5,976 mts. // 10 nindan = 1 eshe (cuerda) 59,76 metros. // 60 nindan = 1 USH 3585,6 metros. // 30 USH = 1 BERU 10.7568 metros
Terreno
La unidad de área básica es la sar, un área de 1 nindan (5,976 m.) cuadrados, o aproximadamente 35,71 metros cuadrados. El área que ella y la ginebra se utilizan como fracciones generalizadas de esta unidad básica.
180 ella = 1 gin // 60 gin = 1 sar (solar ajardinado de 1 metro nindan -. 36 metros cuadrados) // 50 sar = 1 Ubu // 100 sar = 100 sar // 6 Iku = 1 eshe // 18 Iku = 1 fresa // 1 fresa es un área 1 beru de largo por 1 de ancho nindan
Volumen
Unidades de volumen son las mismas que las unidades de superficie y sigue la relación que
1 volumen de unidades = 1 Área de unidad x 1 kush.
Por ejemplo, un volumen-sar es el volumen del sólido con base 1 zona-sar y altura 1 kush (codo).
1 volumen de unidades = 1 Área de unidad x 1 kush.
Por ejemplo, un volumen-sar es el volumen del sólido con base 1 zona-sar y altura 1 kush (codo).
Los ladrillos se consideran sólidos rectangulares tales que 720 ladrillos hacen un ladrillo-sar. Existen numerosos tamaños (bastante estándar) de los ladrillos que se utilizan en los textos de matemáticas babilónicas viejas.
Capacidad: utilizado para la medición de volúmenes de cereales, aceite, cerveza, etc La unidad básica es la sila, alrededor de 1 litro. El sistema babilónico antiguo semi-estándar que se utiliza en los textos matemáticos se deriva de los sistemas de mensuracion muy complejos utilizados en el período sumerio.
Peso
La unidad básica de peso es el maná, de 60 Gin = 498 gramos. // 180 ella = 1 gin / shiqlu (shekel) 8,3 gramos // 60 gin = 1 mana (mina) 498 g. // 60 mana = 1 gu / biltu (talento, la carga ) 29,880 kg.
En pricipio el sistema sexagesimal que alternaban con el decimal,
180 granos =she hacían un siclo (gin), y 60 siclos una mina (mana) haciendo 60 minas el talento (gu-un)
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA sexta
Medidas y pesos de Babilonia (segundo milenio a.C).
Longitud
Más pequeña unidad de longitud es el que ella (barleycorn), de alrededor de 1/356,4 metros.
6 se = 1 shu-si (el dedo) 16,5 mm. // 30 shu-si = 1 kush (codo) 495 mm. // 6 kush = 1 gi / qanu (reed) 297 ctms. // 12 kush = 1 nindan / GAR (varilla .) 5,94 mts. // 10 nindan = 1 eshe (cuerda) 59,4 metros. // 60 nindan = 1 USH 356,4 metros. // 30 USH = 1 BERU 10.692 metros
Terreno
La unidad de área básica es la sar, un área de 1 nindan (5,94 m.) cuadrados, o aproximadamente 35,28 metros cuadrados. El área que ella y la ginebra se utilizan como fracciones generalizadas de esta unidad básica.
180 ella = 1 gin // 60 gin = 1 sar (solar ajardinado de 1 metro nindan -. 36 metros cuadrados) // 50 sar = 1 Ubu // 100 sar = 100 sar // 6 Iku = 1 eshe // 18 Iku = 1 fresa // 1 fresa es un área 1 beru de largo por 1 de ancho nindan
Volumen
Unidades de volumen son las mismas que las unidades de superficie y sigue la relación que
1 volumen de unidades = 1 Área de unidad x 1 kush.
Por ejemplo, un volumen-sar es el volumen del sólido con base 1 zona-sar y altura 1 kush (codo).
1 volumen de unidades = 1 Área de unidad x 1 kush.
Por ejemplo, un volumen-sar es el volumen del sólido con base 1 zona-sar y altura 1 kush (codo).
Los ladrillos se consideran sólidos rectangulares tales que 720 ladrillos hacen un ladrillo-sar. Existen numerosos tamaños (bastante estándar) de los ladrillos que se utilizan en los textos de matemáticas babilónicas viejas.
Capacidad: utilizado para la medición de volúmenes de cereales, aceite, cerveza, etc La unidad básica es la sila, alrededor de 1 litro. El sistema babilónico antiguo semi-estándar que se utiliza en los textos matemáticos se deriva de los sistemas de mensuracion muy complejos utilizados en el período sumerio.
Peso
La unidad básica de peso es el maná, de 60 Gin = 500 gramos. // 180 ella = 1 gin / shiqlu (shekel) 8,3333..... gramos // 60 gin = 1 mana (mina) 500 g. // 60 mana = 1 gu / biltu (talento, la carga ) 30 kg.
En pricipio el sistema sexagesimal que alternaban con el decimal,
180 granos =she hacían un siclo (gin), y 60 siclos una mina (mana) haciendo 60 minas el talento (gu-un)
Coincide con el sistema métrico decimal, habida cuenta que sigue el mismo procedimiemto partiendo desde medidas geodésicas.
:::::::::::.::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA OCTAVA
Medidas hebreas (según la Enciclopedia Judía)
Medidas secas.
1 homer = 10 efas = 30 se'aim = 180 taxis = 720 registros =
364.4lit.
1 cabina = 4 registros = 2.024lit.
1 log = 0.506lit.
Medidas Líquido.
1 cor = 10 piscina = 60 hins = 180 taxis = 720 registros = 364.4 lit.
1 baño = 6 hins = 18 taxis = 72 registros = 36.44 lit.
1 hin = 3 taxis = 12 registros = 6.074 lit.
Talento.
Mina. 1 cabina = 4 registros = 2.024 lit.
1 log = 0.506 lit.
Para ampliar información VER: JewishEncyclopedia.com.
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA UNDÉCIMA
UNIDADES DE MEDIDA EN LÍQUIDOS GRIEGAS
DICHORON = PIE (eubeo o dorio) AL CUBO = 29,7 · 29,7 · 29,7 = 26,198073 litros o kilos
DICHORON ES 26198,073 mililitros o gramos
A su vez, el Diochoron es 2/3 de ánfora de lo que nos quedan los valores:
Metretes (ánfora griega).. 144 cotilas... 1,5 Dichoron = 39,2971095 litros o kilos.
Dichoron... 96 cotile... Pie de 29,7 ctms al Cubo..... = 26,198073 litros o kilos.
Chous.... 12 cotilas..... = 3,274759125 litros o kilos
Hekteus .... 2 cotilas.... = 0,5457931875 litros o kilos (545,7931875 gramos)
Cotila.... 24 listron.... = 0,27289659375 litros (272,89659375 gramos)
Hemikotylion... 12 listron = 0,136448296875 litros (136,448296875 gramos)
Oxivafon ... 6 listron... = 0,0682241484375 litros (68,2241484375 gramos)
Kyathoskuathos... 4 listron = 0,045482765625 lit. (45,482765625 gramos)
Mystron... 2 listron ... = 0,0227413828125 litros (22,7413828125 gramos)
Listron .... 1 LISTRON... = 0,01137069140625 litros (11,37069140625 gramos)
UNIDADES DE PESO EN METAL
Desde la Mina = Hekat griega = Hekteus de 454,82765625 gramos
Óbolo.... 1/6 Dracma...= 0,75804609375
Dracma.... 6 óbolos.... = 4,5482765625 gramos
Mina.......100 Dracmas = 454,82765625 gramos
Talento....60 minas...... = 27,289659375 gramos
UNIDADES DE PESO EN METAL desde Talento = Dichoron
Pie de 29,7 ctms al Cubo..... = 26,198073 litros o kilos = Talento.
Óbolo.... 1/6 Dracma...= 0,72772425
Dracma.... 6 óbolos.... = 4,3663455 gramos
Mina.......100 Dracmas = 436,63455 gramos
Talento....60 minas...... = 26,198073 gramos
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
TABLA DE CONCORDANCIA duodécima
Diferentes medidas griegas y romanas:
Unidades Griegas.
(Reinach, 1880)
Dedo 1/16 de pie
Cóndilo 1/8 de pie
Palma 1/4 de pie
Pie ático u olímpico (Error: pone 0,368) 0,308 m
Codo 1,5 pies
Paso 2,5 pies
Braza u Orgia 6 pies 1,85 m
Pletro 100 orgias
Estadio olímpico 6 pletros (1/8 de Milla romana) 184,97 m
(Glotz, 1948)
Sistema eginético
Pie de Phidon o Babilónico o de Filetero
Dóricos, Peloponeso, Grecia Norte
330 mm 2/3 del codo babil.
Sistema euboico
Eubea, Corinto, Jónicos, Atenas (romanos)
297 mm 3/5 del codo babil.
(Jodin, 1975)
Pie de Delos o de Epidauro 327 mm Codo 0,490 m
Pie de Corinto 297 mm Codo 0,445 m
Pie ático u olímpico= 10 / 9 del pie babilónico 368 mm Codo 0,552 m
(Chouquer; Favory, 1993)
Gyes (Superficie) Campo que se labra en un día
Tetragyon 4 gyes
(Docci, 1994)
Palma 0,0740 m
Pie 4 palmas 0,2960 m
Codo 1,5 pies 0,4440 m
Paso 2,5 pies, 5/3 de codo 0,7400 m
Pletro (jugero) 40 pasos 29,60 m
Estadio 6 pletros 177,60 m
Pie jónico 0,2775 m
Pie olímpico 0,3080 m
ROMANAS Y ALGUNAS GRIEGAS:
ESTADIO ÁTICO............................184,98 (PROCEDE DEL PIÉ babilónico= 0,3083 x 600)
ESTADIO OLÍMPICO ................... 192,27 (pie 0,32045 x 600)
PIE GRIEGO ática ..................................... 0,3083
ESTADIO GRIEGO común ........................ 184,10 (6000 PIES)
PARASANGE GRIEGO ................ 5523 (30 ESTADIOS)
PIÉ ROMANO ................................ 0,29466
PASO ROMANO ........................... 1,4733 (5 PIES)
CODO GRIEGO.............................. 0,444 IGUAL AL CODO PERSA, DIVIDIDO EN 24 DEDOS Y 6 PALMOS, ES EL QUE ADOPTA ROMA
CODO ROMANO .......................... 0,444 VIENE DE GRECIA
CODO GRIEGO OLÍMPICO ......... 0,4806
ESTIMACIÓN DEL MERIDIANO
600 pies = 1 Estadio // 600 estadios = Grado // 360 Grados = Meridiano de 39.955.680 metros
600 Pie (0,3083 m) = Estadio de 184,98 mts
Estadio x 600 (Grado de 110.988 metros)
360 Grados = 39.955.680 metros (error frente a 40.000.000 = 44 kilómetros aprox.)
ESTADIO ÁTICO (184,98 mts) = 1/8 de Milla Romana
-
Comentario por Luis Castaño Sánchez el mayo 8, 2016 a las 1:45am
-
Buenas noches:
Tras bastante tiempo sin entrar en Terrae con asiduidad acabo de entrar hace un rato y he llegado a este artículo en el que, entre otros muchos aspectos, se trata sobre Metrología.
Habiendo descubierto en 2011 el Canon Original, unidad central del Sistema de Medidas Antiguo, vengo revisando desde entonces la totalidad de la disciplina partiendo de dicho modelo humano.
Debido a ello me veo obligado a discrepar con algunos de los planteamientos y afirmaciones vertidos en este artículo, así como a proponer determinadas rectificaciones a ellos.
Espero que se entienda que el objetivo es en todo momento aportar una claridad de ideas muy necesaria en la disciplina. (Enlaces sobre mi investigación al final de este largo comentario):
Sobre el “Hombre de Vitruvio”:
Lamentamos disentir enormemente de muchas de las afirmaciones realizadas sobre el llamado “Hombre de Vitruvio” así como del análisis del mismo realizado por el autor del artículo. Como ya explicamos en nuestro trabajo “Metrología Histórica: Una nueva propuesta” y hemos demostrado posteriormente en nuestra investigación:
1/ El modelo humano de Leonardo NO es el Hombre de Vitruvio. La postura del Hombre en T sí es la misma que describió Vitruvio en sus Diez Libros de Arquitectura, pero la postura circular que describe Vitruvio es la de un Hombre en ( | ). Dicha postura se encuentra previamente en Egipto y llega hasta Vitruvio. Posteriormente el texto vitruviano es mal interpretado y, probablemente, a través del Hombre en (Y) planteado por Giacomo Andrea de Ferrara, Leonardo propone un Hombre en (X) que no coincide con el descrito por Vitruvio en su tratado.
2/ En contra de lo que suele decirse Leonardo NO trazó su modelo empleando Phi. Simplemente empleó una línea con las medidas de su época (ver la base del cuadrado), trazó una cuadrícula y sobre ella trazó el Hombre en T. A partir de él (tal como explica en sus notas) trazó el Hombre en X.
3/ En él no sólo se muestran las proporciones perfectas del cuerpo humano. El modelo TAMBIÉN recoge las medidas exactas que se empleaban en la Antigüedad y que vienen desde muy atrás en la Historia (Sumer, como mínimo) tal como venimos demostrando desde 2011. El modelo corresponde a un Hombre de 1'80 metros de altura y es ese valor el que nos da la equivalencia de las medidas del Sistema de Medidas Antiguo a nuestro Sistema Métrico Decimal.
4/ Por cierto, hablando de proporciones, es fundamental señalar que éstas se basan en el cuerpo humano y en concreto es fundamental señalar que Leonardo recoge la correcta proporción del Pie natural (1/7), proporción que nos ofrece un valor de Pie de 25'65 cm, valor que aparece ya en el Patrón de Nippur (Siglo XXVII AC, Sumer) y se transmite con todo el modelo. Esta proporción correcta es fundamental ya que pone en evidencia que muchas (prácticamente todas) de las medidas denominadas habitualmente “Pies” no son tales Pies, sino simplemente medidas que reciben ese nombre. Se hace obligado por tanto una revisión completa de la disciplina para corregir numerosos errores (como mínimo conceptuales), errores que por desgracia a día de hoy se siguen difundiendo y perpetuando.
5/ El análisis propuesto para el modelo de Leonardo no se sostiene: no se reproduce la totalidad del documento, no se señala la regla bajo el cuadrado, no se indican las medidas de la misma, no se traza la cuadrícula sobre la que se sustenta el Hombre en T, no se parte de él (y de las notas) para trazar el Hombre en X, etc. En definitiva, el análisis no se corresponde con el documento original. (ver nuestro análisis en "Metrología Histórica: Una nueva propuesta").
6/ Afirmar que la base matemática más perfecta es la decena nos parece, cuando menos, arbitrario.
7/ Afirmar que “todas las medidas usadas por grandes civilizaciones en la Antigüedad son patrones geodésicos tomados después de medir el arco terrestre” nos parece tremendamente discutible. Como ya hemos explicado en algún debate sobre este tema, las primeras unidades de medida de longitud (Pulgada, Pie, Codo y muchas otras) nacen del estudio de las proporciones ideales del cuerpo humano y de sus miembros (de ahí los nombres de esas medidas), de la adopción de una altura fija de Hombre como estándar y del registro de dichas medidas en barras metálicas (Patrón de Nippur Siglo XXVII AC Sumer) o en listones de madera (Patrón de Maya Siglo XIV AC Egipto). O, por citar a Protágoras, “El Hombre es la medida de todas las cosas”. Los patrones, por tanto, no surgen después de medir el arco terrestre. En nuestra opinión es más bien al contrario. Se estudia el cuerpo, se establece un modelo, se graban sus medidas en patrones y, posteriormente, se emplea ese sistema de medidas para medir el entorno, entorno que puede incluir el arco terrestre.
8/ Dicho todo esto, existe una confusión habitual en Metrología Histórica (y en la que el autor incurre) que consiste en llamar Pie o Codo a muchos patrones. Por ejemplo podemos leer:
“Estableciendo en Saqaara como medida sagrada el Codo Real de unos 52,46 centímetros. Un patrón métrico que no cambia prácticamente en toda la historia de Egipto.”
Como suele ser habitual se produce aquí una confusión múltiple. El Codo humano (basado en el cuerpo) mide desde la articulación del Codo hasta la punta de los dedos en la postura en T, es decir, 6 Palmas = 45 cm. Algunos Patrones que recogen las medidas egipcias (Patrón de Maya, Museo del Louvre; Patrón de Kha, Museo de Turín) miden 7 Palmas = 52'5 cm (pero son Patrones, no Codos). Y la medida Codo Real (recogida en muchos textos de autores antiguos) corresponde a 8 Palmas (60 cm) o 32 Dedos (57'6 cm). Mientras no se distingan claramente estos puntos jamás saldremos de las enormes confusiones que reinan (aún a día de hoy) en Metrología.
9/ En cuanto a las tablas de concordancia propuestas al final del artículo habría que revisarlas en su totalidad (como de hecho ocurre con la gran mayoría de tablas propuestas en Metrología). En nuestro caso venimos revisando infinidad de trabajos desde 2011 con la ayuda del modelo humano correcto. Dicho sea de paso, resulta incoherente afirmar (como hacen la mayor parte de los estudiosos) que las medidas antiguas eran antropométricas y luego estudiarlas sin emplear ningún modelo humano para ello. Como consecuencia de ello puede comprobarse con facilidad que se llama Pie y Codo a infinidad de medidas, debido a que no se han estudiado en relación al cuerpo. Sin embargo, y queremos dejar constancia de ello para intentar evitar la difusión de errores, el Pie natural (1/7) mide 25'65 cm y el Codo (¼) 45 cm. Y por supuesto el Hombre (el modelo que se empleó en origen) mide 1'80 m como venimos demostrando en nuestros trabajos desde 2011. Sin partir de ese modelo (y sus equivalencias) en Metrología Histórica se seguirá avanzando a ciegas.
10/ Para no extendernos en exceso propondremos una revisión sólo de las primeras medidas de longitud recogidas. Todas ellas pueden explicarse con el modelo de 1'80 metros (24 Palmas = 1'80):
Dedo 18,7 mm. → Dedo = 1'875 cm (Para ser precisos el Dedo mide 1'800 cm *)
Palma 4 dedos 74,8 mm. → Palma = 7'5 cm (4 Dedos = 7'2 cm *)
Spanna 3 palmas 224,4 mm.→ Palmo = 3 Palmas = 22'5 cm (12 Dedos = 21'6 cm *)
Pie 299,2 mm. → El Pie natural (1/7) mide 25'65 cm.
La medida de 30 cm (4 Palmas) NO es un Pie.
Codo 6 palmas 448,8 mm. → Codo = 6 Palmas = 45 cm.
Codo real 7 palmas 523,6 mm. → 7 Palmas = 52'5 cm. Esta medida de 7 Palmas NO es un Codo.
8 Palmas = 60 cm; 32 Dedos = 57'6 cm. (Codo Real)
* Los textos recogen que el Dedo (1'8 cm) se divide en 4 Granos (4'5 mm) y el Grano en 6 Pelos de camello (0'75 mm). Ese Pelo de camello (0'75 mm) es la Marca entre los Dedos en los Patrones.
Por último, dejamos algunos enlaces a entrevistas en las que explicamos nuestra investigación y en las que puede observarse el análisis correcto del modelo de Leonardo así como enlaces a nuestra página en www.academia.edu y a nuestro blog para quien quiera consultar nuestros trabajos:
RNE: https://www.youtube.com/watch?v=UjtQ5JQZGnc
Onda Cádiz: https://www.youtube.com/watch?v=DjVi0u0rySY
Onda Luz: http://ondaluz.tv/jerez/ventana-a-la-historia/2-27-18112015-luis-ca...
Cádiz Directo: http://terraeantiqvae.com/profiles/blogs/luis-castano-solo-busco-qu...
Academia: https://independent.academia.edu/LuisCasta%C3%B1o
Blog Metrología Histórica: http://metrologiahistorica.blogspot.com.es/
Comentar
Bienvenido a
Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae
TRANSLATE BY GOOGLE
Busca en Terrae Antiqvae
Recibe en tu correo los últimos artículos publicados en Terrae Antiqvae -Boletín Gratuito-
Donaciones
Terrae Antiqvae es una Red Social sin ánimo de lucro. Necesitamos tu apoyo para el mantenimiento del sitio. Apadrina esta Comunidad
Publicidad by Google
Lo más visto
Patrocinador: SMO Sistemas
Nuestro Canal de Vídeos en YouTube. ¡Suscríbete!
Síguenos en Redes Sociales: Facebook y Twitter
¡Gracias por visitarnos! ¡Bienvenid@!
Estadísticas desde 12 de noviembre de 2014.
Derechos de Autor:
Terrae Antiqvae® is licensed under a Creative Commons Reconocimiento-NoComercial-SinObraDerivada 3.0 Unported License.
Información legal: Terrae Antiqvae® es Marca registrada por José Luis Santos Fernández. Marca nº 2.679.154 - Clase 41, Madrid, España. Reservados todos los Derechos. En Internet desde Julio de 2001.
Normas de la Comunidad (Aviso Legal): Netiqueta - Términos de servicio
© 2024 Creado por José Luis Santos Fernández.
Tecnología de
¡Necesitas ser un miembro de Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae para añadir comentarios!
Participar en Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae