DEBIDO A LA EXTENSIÓN DEL ARTÍCULO, LO HEMOS QUE DIVIDIDO EN TRES PARTES, SIENDO ESTA LA TERCERA. PARA LEER LAS DOS ANTERIORES CONSULTAR EN MI PÁGINA.
PARTE TERCERA; continúa:
F) La Escala Universal, inversa y progresando en razón “al doble”:
.
Tomando la longitud de Mercurio al Sol como un tono inicial (la “primera nota”); observamos que ese “intervalo” es proporcional a todas las distancia entre los planetas y el Sol. Tal como sucede -por ejemplo- en la longitud entre la Tierra y el astro mayor, que sería de 10/4 (58 mK. · 10/4 = 145 mK.); o en la distancia desde Venus al Sol, que se correspondería con 7/4 del tono inicial (Mercurio-Sol).
.
Por todo ello, la primera serie de funciones que encontramos es:
58.000.000 millones K …....................SOL-MERCURIO (tono inicial)
58 · 7/4 = 101,5 …................................SOL-VENUS
58 · 10/4 = 145 ….…...........................SOL-TIERRA
58 · 4 = 232 …................................SOL-MARTE
58 · 7 = 406 …................................SOL-CERES
58 · 13 = 754 …................................SOL-JÚPITER
58 · 25 = 1450 …...............................SOL-SATURNO
58 · 49 = 2842 …..............................SOL-URANO
58 · 73,5 =4263 …................................SOL-NEPTUNO
58 · 97 = 5626 …................................SOL-PLUTÓN
58 · 193= 11194 …................................SOL-SEDNA
58 · 385 =22330 …............................... SOL-Planeta pitagórico.
.
Podremos observar, la serie es tal como la hemos descrito, del doble de la anterior, menos la distancia primera. Así, siendo el primer intervalo tomado como 1 se obtiene la siguiente serie, aunque siempre con la variación del segundo planeta en cada Octava (cada ocho).
.
1 ........................................distancia de Mercurio
(1 · 2) – ¼) = 7/4 …............distancia de Venus
(7/4 · 2) - 1 = 10/4 …..........distancia de Tierra
(10/4 · 2) -1 = 4 …..............distancia Marte
(4 · 2) – 1 = 7 ….................distancia Ceres
(7 · 2) – 1 = 13 …...............distancia Júpiter
(13 · 2) – 1 = 25 ….............distancia Saturno
(25 · 2) – 1 = 49 ….............distancia Urano
Comienza la Segunda Octava o serie de planetas, por lo que contiene una irregularidad en la distancia de Neptuno igual a la que contiene Venus:
(49 · 2) – ¼ (49 · 2) = 73,5 …............distancia a Neptuno
(49 · 2) – 1 = 97 …..............................distancia a Plutón
(97 · 2) – 1 = 194 …............................distancia a Planeta pitagórico
.
Tal como lo hemos visto, la serie progresa en relación a (2x-1) siendo “x” la distancia entre mercurio y el Sol. Aunque ha de variar en la primera longitud (Venus Sol), pues si “x” es 1, (2x-1) sería igual a 1 de nuevo (Mercurio-Sol). Pero también cambia en la Octava distancia (Neptuno-Sol), todo lo que lleva a ver que su ritmo es muy semejante al de las Escalas musicales. Tanto que la diferencia entre la primera y la segunda nota (Mercurio-Sol y Venus-Sol) está en relación a las proporciones de los temperamentos antiguos, siendo ¾ (o bien menos ¼) . Al igual que sucede entre Urano y Neptuno, cuya diferencia de longitudes es también de ¾.
.
De ello, podemos considerar el Sistema Solar como una Escala, aunque al progresar en razón al doble (posicionándose cada cuerpo celeste casi al doble del anterior), las notas irían en diferentes Octavas; subiendo en cada caso a otra superior. Es decir, que el DO primero (Mercurio-Sol) estaría en una primera Octava (más baja), esta nota se multiplicaría por dos, llegando al DO2 aunque al restar un tono (cuando quitamos ¼ al doble) habríamos llegado a un SI.
Su fórmula sería (DO1 · 2) – (un tono) = SI2
Por ello, Venus-Sol se correspondería con la siguiente nota, que como vemos es SI2 .
A continuación, este SI2 vuelve a doblarse, llegando al SI3 desde donde se baja una nota; por lo que Tierra-Sol se corresponderá con un LA3 .
Del mismo modo sucede en la siguiente longitud, que debemos multiplicarla por 2 y restarle 1, por lo que se llega a LA4 ; resultando finalmente que Marte-Sol es un SOL4 . Continuando la serie que completaría el DO8 (el siguiente DO) en Urano. Por lo que al comenzar la nueva Octava, el SI9 (Venus-Sol) contendría la misma irregularidad que tiene el SI2 (Neptuno-Sol).
.
De ello, tomando Tono inicial como la distancia de Mercurio al Sol (58 mill.Kmts.); la ecuación de progresión, expresada como notas es:
(Tono · 2) – Tono = longitud al siguiente planeta.
A excepción en cada Octava, de que la nota inicial (SI) es:
(Tono · 2) – x/4 = longitud de primer nota en cada Octava (SI2 , SI8 , SI16 etc)
.
.
IMAGEN ARRIBA: Dibujo mío con el Sistema Solar visto como una “estátera” (balanza) en la que el equilibrio de los planetas va en función de armonía musical. Como podemos ver, existe una proporción plenamente relacionada con los intervalos de una Escala. Tanto que cuando comienza la segunda serie de “notas” (planetas) vuelve a tener la misma irregularidad que al principio. De ello, Mercurio actuaría como Urano (ambos DO) y Venus igual que Neptuno (SI2 y SI8) . Por lo demás, siguiendo estas proporciones, debería existir un planeta a la distancia que hemos marcado (el doble de la de Sedna menos la de Mercurio) a 22330 millones de kilómetros del Sol.
.
IMAGEN ABAJO: La Escala musical en la primera serie de Planetas (desde Mercurio a Urano). Se trataría de una escala inversa (do-si-la-sol-fa-mi-re-do) porque cada planeta dista el doble del anterior, menos un tono (el intervalo inicial = Mercurio-Sol). Ello implica que cada vez sube a una Octava diferente y baja una nota, todo lo que supone la serie que hemos descrito (do1-si2-la3-sol4-fa5-mi-6re7-do8); donde cada tono pertenece a una Octava diferente y superior.
.
G) La ley Titius-Bode y el órden cósmico:
.
Las conclusiones antes expuestas parten de una teoría hallada por Titius y que Bode divulgó años más tarde (sin citar la fuente dónde la había tomado). Sobre ella decíamos en mi trabajo “Creación, temperación e improvisación” que: La ley llamada de Bode-Titius, fue propuesta en 1766 por J. Daniel Titius, quien no le debió otorgar demasiada importancia; aunque pudo vaticinar que encontrarían un planeta donde posteriormente hallaron Urano. Tras el fallecimiento de éste, Johan E. Bode en 1772 la publica, sin mencionar a su verdadero autor y poco después se llega a demostrar que era cierta. Pues -efectivamente- en 1781 William Herschel descubrió Urano donde Titius había intuido que tenía que haber un cuerpo celeste, hasta entonces desconocido. Medio siglo después y cuando descubren en el lugar donde la ley de Titius marcaba otro astro, el Asteroide Ceres (hacia 1801); se confirma la veracidad de esta teoría. Pese a ello, desde hace unos decenios se ha desechado como idea, tanto que no se considera a Plutón un planeta.
.
Se basa en que cada cuerpo celeste del Sistema Solar guarda una distancia correlativa con el siguiente y en una progresión igual. Modernamente se expresa con teoremas muy sofisticados, pero es tan simple como el planteamiento que a continuación describimos:
.
Tomemos como progresión los números 0, 3, 6, 12, 24, 48, 96, 192. Dicha sucesión sencilla nace desde 0, añadiendo 3 y aumentando (3 x 2); x 2; x 2; x 2, etc.
Sumemos después 4 a los números que salgan sucesivamente.
Para este caso, la medida de distancia de referencia que será: de la Tierra al Sol, que cifraremos como diez. Es decir, longitud de la Tierra al Sol = 10.
En razón a todo lo apuntado, calcularemos las distancias entre los planetas así:
Planetas …..............Número de Titius................. Distancia real (al Sol)
Mercurio..................... 0 + 4 = 4................................... 3,9
Venus......................... 3 + 4 = 7................................... 7,2
Tierra.......................... 6 + 4 = 10 …............................ 10
Marte.......................... 12 + 4 = 16............................... 15,2
Ast Ceres.................... 24 + 4 = 28.............................. 27,7
Júpiter......................... 48 + 4 = 52............................... 52
Saturno....................... 96 + 4 = 100 ….........................95,4
Urano.......................... 192 + 4 = 196 ….......................192
Neptuno*........ …........ 384·3/4 = 291............................300,6
Plutón.......................... 384 + 4 = 388 ….......................394,4
.
Continuábamos diciendo en nuestro estudio-conferencia que: Esta ley tuvo gran importancia y desarrollo en toda la astronomía del siglo XVIII, pues cuando se planteó aún no había sido encontrado Urano. Los astrónomos observaron allí donde debiera haber un planeta según Bode-Titius y en 1781 se descubrió esa nueva esfera (Urano). Todo ello supuso un gran regocijo para Bode, que se hizo famoso por su ley (tomada de Titius). Aunque inmediatamente se refutó la teoría porque entre Marte y Júpiter no había cuerpo celeste alguno; pero encuentran poco más tarde un campo de Asteroides, confirmando completamente la ley. El pitagorismo vuelve a plantearse en el siglo XIX como una realidad cósmica, que puede explicar estas proporciones. En relación a ello, Benito Montú (1761-1814) construye la llamada “Esfera Armónica”, ideada por él, que medía las distancias de los planetas y su relación con los intervalos de los sonidos, un invento por el que el Gobierno francés pagó 12.000 francos en 1802.
.
Pese a todo, en 1846 se descubre Neptuno, que no cumple la ley, pues está justo en mitad de la distancia al lugar que debía haber ocupado el siguiente planeta. Tras el hallazgo de este último, se decide que la Ley de Titius-Bode no tiene ni fundamento ni efecto real, por lo que se invalida como hipótesis científica. Pero en 1930, vuelve a aparecer un nuevo “planeta” en escena que será Plutón, y que curiosamente sí guarda de nuevo las proporciones. Además se estudia el caso de que entre Plutón y Urano (a medio camino) se había encontrado Neptuno, aquel que no cumplía la ley de Titius pero aparece en su centro (pues la media distancia entre ambos es a 293,2 y ese planeta está en el 300,6). Hemos de añadir que, debido al tamaño y longitudes en que van apareciendo los últimos planetas, aunque nos parezca que tienen altos errores, el porcentaje de éste en relación a sus distancias es mínimo. Citamos, por ejemplo, que en la diferencia de 196 a 192 (Urano) hay apenas un 2%; y de 388 a 394,4 (en Plutón) hay tan sólo, algo mas de un 1,5%. A todo ello ha de señalarse que las órbitas son elípticas, por lo que las distancias reales son medias, no exactas...
.
.
IMAGEN ARRIBA: El Sistema Solar representado como una estátera, cuyos equilibrios se deben a una armonía semejante a la musical. La distancia de los planetas en este caso está en relación a la Ley de Titius. . IMAGEN ABAJO: El “arpa celeste” y sus notas, expresadas sobre las teclas de un piano. Vemos como el primer tono sería el DO1 (de Mercurio al Sol); tras el que sube una Octava, para bajar una nota; por lo que Venus-Sol se correspondería con un SI2 (“Si” en la siguiente Octava). Lo mismo sucede en la distancia del Sol a la Tierra, que es el doble de la anterior, menos una nota (restando el tono Mercurio-Sol); correspondiendo a un LA3 . Así sucesivamente, hasta llegar a Sedna, que estaría ya en la Octava 11º (muy por encima de las ocho Octavas que comprende el piano) y sería un SOL11 . .
.
H): El Tiempo y el ritmo; razones de una armonía Musical:
.
La explicación científica a estas distancias proporcionales entre los planetas se basa en un hecho descrito como “Resonancia Orbital Gravitatoria”. En razón a que todo cuerpo celeste girando alrededor de un centro orbital (en este caso, el Sol) cuyo ciclo al completar cada vuelta es “x”. Difunde una masa -fuerza gravitatoria- que tiende a estabilizar o hacer salir de sus órbitas los astro cercanos y de menor tamaño, cuyo ciclo sea igual, múltiplo o fracción de “x” (siendo “x” como dijimos: La duración del mayor en completar su órbita sideral). Es decir, que si la Tierra gira alrededor del Sol en unos 365,25 días; todos los cuerpos celestes menores a la Tierra y cuya vuelta completa de traslación tenga un periodo proporcional a este (365,25 días, dividido o multiplicado por un número entero). Reciben un “impacto de resonancia” que les va equilibrando o desencajando en sus órbitas, hasta sacarlos o bien estabilizarlos en ellas (tendiendo a comportarse como el cuerpo mayor o bien saliendo de su órbita -para estrellarse contra otros astros-). Ello obliga a cada cuerpo celeste a situarse en una circunferencia relativa a la duración de los ciclos de los demás planetas; que no solo ejercen individualmente el efecto de su masa y su distancia, sino donde los cuerpos mayores someten a los menores a desplazarse, girando a un mismo ritmo.
.
Para que entendamos un poco lo que puede ser esta “resonancia orbital” lo explicaremos como un lanzador de martillo olímpico. Debido a que cuando un deportista toma una “resonancia perfecta” con el peso que lanza al girar (su ritmo e inercia), el martillo llega mucho más lejos. Lo que se produciría por un efecto semejante a lo descrito anteriormente. Pues en el momento que el atleta gira para lanzar, rotando en círculos; estos deben ser ritmicamente iguales a la inercia que tiene el peso; y de no ir acorde en ritmo, la fuerza centrífuga quedará muy reducida. Visto así, un igual ritmo centrífugo sería lo que contienen aquellos planetas que giran alrededor del Sol en ciclos paralelos (en número igual o múltiplo de días). Por lo que aquellos que tienen mayor masa tienden a absorber a otros menores, en un mismo ritmo de rotación; de igual modo que el lanzador del martillo olímpico logra llegar mucho más lejos cuando se acopla perfectamente a la inercia que él mismo da al peso que tira.
.
Entendida la anterior premisa, se comprende por qué no hay planetas que roten alrededor del Sol con un mismo ciclo. Pues si dos cuerpos celestes dieran en igual tiempo una vuelta completa entorno al astro rey; el mayor de aquellos terminaría desplazando al más pequeño, hasta sacarle de su órbita. Por todo ello, la relación masa y distancia no es solo lo que cuenta en la disposición de las longitudes de los planetas; ya que hay además un factor extraño y ajeno al Espacio: EL TIEMPO. Pues cuando dos cuerpos celestes giran a igual ritmo alrededor del Sol, termina expulsando o absorbiendo uno al otro. Ello obliga a incorporar una segunda categoría a la ley gravitatoria; “el tempo” que en música es lo mismo que el ritmo; los que demostraría como el Universo actúa realmente con una armonía musical plena, no solo en relación a sonidos (tonos o notas como una Escala).
.
Llegando a este punto nos debemos plantear si el Tiempo era una sucesión de Espacios (tal como Kant lo expresaba) o existe por sí mismo. Pues si aquel ritmo de giro es igualmente capaz de variar las coordenadas astrales (siendo capaz de expulsar planetas de una órbita); el Tiempo -como categoría- existe por sí mismo y no precisa del Espacio para “ser”. Por lo que no podemos concebir el Tiempo como una sucesión de Espacios, siendo posible que aún sin el Espacio hubiera Tiempo. Más aún, nacería de esta hipótesis una tercera “categoría” (no prevista) que sería la Velocidad; ya que es la que en este caso determina que los planetas orbiten en armonía (unos alrededor del otros). Todo ello, unido a la masa y a la distancia, que afecta al hecho de que un cuerpo celeste con más masa, expulse de su órbita a uno más pequeño (decenas, centenas o miles de millones de años). Siendo así, las categorías serían tres: Espacio, Tiempo y Velocidad. Factores que la física nos ha enseñado como combinados se expresan mutuamente: Velocidad = (Espacio : Tiempo) // Espacio = (Velocidad : Tiempo) // Tiempo = (Espacio : Velocidad).
.
.
SOBRE ESTAS LINEAS: Representación de la cuerda 1ª de la guitarra como si fuera una balanza de la que se cuelgan pesos, hasta lograr su afinación a modo pitagórico. Observemos cómo en el primer caso bastaría con poner su centro gravitatorio en medio (exactamente) lo que supondría hallar la misma nota una Octava más alta. Es decir, pulsar en el milímetro 330; por lo que siendo MI el 660, en este donde hemos situado el punto central de la balanza volvería a sonar MI. Ello hace que para equilibrarlo, se precisa de un peso igual, habida cuenta que las notas son las mismas.
.
En la segunda viñeta pasamos ya a calcular la nota siguiente armónica, que se halla (como sabemos) cortando la cuerda de nuevo en su mitad y añadiéndole el valor de antes. Es decir {(MI : 2) + MI}:2 = {(330 : 2) + 330} : 2 = (165 + 330) : 2 = 247,5 mm.. Lo que significa un LA, que es el ese tono armónico con MI (su Quinta) y que en una balanza se representaría del modo que el dibujo enseña: Mostrada en la viñeta en que pone “2ª NOTA”. Viéndose que el peso y la distancia de un lado de la balanza, sería 1/3 mayor que el del otro.
.
La tercera armónica la hallaríamos de nuevo buscando el centro de 247,5 mm. y sumándole 247,5 mm. (partiendo su resultado por dos, para transportarla a igual Octava). Siendo el total {(LA/2 + LA) : 2} : 2 = 185,625 mm. y que es donde se sitúa el RE. Observándose como en RE ya habríamos de situar la balanza a 16/9 del centro y poner una pesa 16/9 mayor a la del lado contrario. La serie de doce notas sería completada de igual manera, hasta llegar al tono 12º.
En el dibujo anterior vemos como distancia y pesos son proporcionales al sonido, de forma paralela y exacta.
.
BAJO ESTE PÁRRAFO: Por todo cuanto vamos viendo, la balanza y la mujer con la estátera de peso en la mano se convirtieron en el símbolo de la equidad, la justicia, la ley y hasta del bien. Consecuentemente los dioses ligados a la balanza (como Maat, Aequitas, Themis, Dike, Fas, Iustitia, Kairós etc.) fueron deidades representativas del equilibrio social, del bien, de la justicia y de la ley. En imagen, un antoniniano del emperador Constantino con la diosa de la equidad en el reverso; a su lado una de las múltiples representaciones de la bellísima Maat egipcia.
Continuando con la el planteamiento anterior, muy fácil nos será ver en la música la diferencia entre Espacio, Tiempo y Velocidad; todo lo que se comprende al ser el Espacio el tono -la nota-, el Tiempo, el mismo tempo regulado en cada compás; y finalmente la velocidad, la duración de cada nota (blanca, negra, corchea, semicorchea etc). De tal manera, entenderíamos por qué notas tocadas con un mismo tempo y de una igual duración, se superponen unas a otras, haciendo que las más graves absorban siempre el sonido de las que son idénticas, pero más agudas. Ello se referiría a la “resonancia” aunque en este caso esa absorción de unas notas frente a otras se produce por lo que denomina “simpatía acústica”. Un hecho que implica a su vez que si hacemos sonar una misma nota, la onda acústica afectará a las armónicas que les rodean. Por lo que si situamos un violín sobre un piano y tocamos en el teclado de este tonos en los que afinan las cuerdas del violín, el instrumento puesto allí encima comenzará a vibrar y a sonar.
.
Algo semejante es lo que se produce con la “resonancia gravitatoria”, que nace cuando dos astros giran entorno al Sol en un periodo de tiempo igual o equivalente (múltiplo o divisible). Un hecho que surgiría en razón de esa velocidad equilibraba y semejante, debido a la atracción de su masas -cuando dos o más cuerpos dan vueltas alrededor de un punto central, en un “tempo equivalente”-. Momento en el cual el de mayor masa absorbe la velocidad paralela, terminando por equilibrar o desajustar (hasta expulsar de su órbita), al de menor peso. Aunque realmente como mejor puede entenderse esta “resonancia gravitatoria” sería pensando qué sucede cuando hacemos girar sobre nuestro dedo índice un pequeño aro; imaginando qué pasa si a la vez oímos una canción y seguimos el ritmo con el mismo dedo. Todo lo que supone que al mover nuestra mano en golpes equitativamente iguales (casi perfectos en tempo), el aro se acelerará de un modo que; o saldría despedido o bien se estabilizaría perfectamente, situándose en un punto del dedo (sin caer hasta que parásemos).
.
Tras los anteriores paralelismos y después de tantos ejemplos, con los que hemos entendido qué es la “resonancia gravitatoria” podemos pasar a preguntarnos: -¿Qué produce en verdad la resonancia gravitatoria, si no es propiamente la masa y la distancia?-. Siendo así, podremos preguntarnos qué “resuena gravitacionalmente” cuando dos cuerpos celestes giran alrededor del Sol a un ritmo semejante, para que uno afecte al otro. Cuestión que tan solo deja como respuesta “el número”; puesto que esta “resonancia orbital” se produce cuando el periodo necesario para rotar sobre el Sol es el mismo, o bien múltiplo del que otro astro tiene. Siendo la coincidencia en un número (múltiplo o fracción) de días, horas o años para girar alrededor del astro central; lo que marca que unos y otros planetas se vean afectados finalmente en su disposición.
.
Todo lo que implica que la “música de las Esferas” no sería propiamente acústica sino numérica; marcada por el Espacio, el Tiempo y la Velocidad, que reguladas en diferentes periodos, en distintos pesos, distancias, ciclos y etc van conjugando esa sinfonía celeste. Componiendo un poema conjugado en números (cíclicos, de masa, fuerzas...) que define lo que es una creación armónica, cuya imagen y semejanza sería la de la música. Tan parecida en sus valores y formas de medir los secretos del equilibrio en una balanza o a la física de las ondas sobre un vaso de agua. Puesto que el sonido no existe en el Espacio, ya que la onda acústica necesitaría de atmósfera para transmitirse. De tal modo, en el vacío nada puede oírse; motivo este por el cual el tremendo ruido de los planetas al trasladarse no llega hasta nosotros. Por lo tanto, tampoco puede existir música propiamente dicha en el Universo, por cuanto estas “sinfonías celestes” estarían basadas en el número (confirmado en distancias, tempos, pesos y etc.).
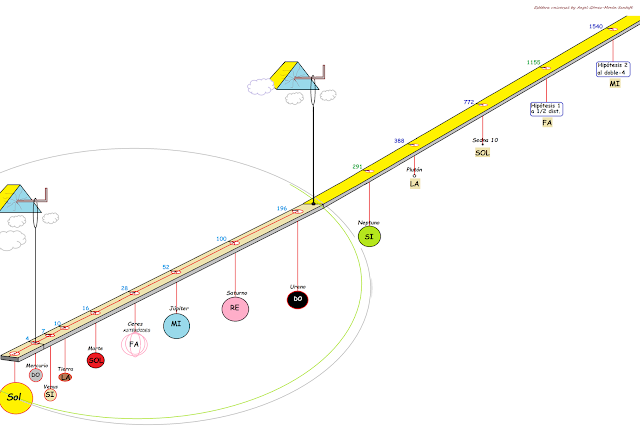
SOBRE Y BAJO ESTAS LINEAS: Disposición de los planetas del Sistema Solar, en forma de Octavas y con las distancias ya marcadas en proporciones iguales. En la imagen superior tenemos algunas características de planetas que nos pueden hacer entender cómo y por qué se produce la “resonancia orbital” ya que:
-Júpiter y Saturno tienen los periodos orbitales en coincidencia de 5/2 -por cada 5 vueltas al Sol que da Júpiter, Saturno habrá completado 2-.
-Por su parte, la enorme proximidad al Sol de Mercurio, hace que su periodo de rotación que sea 2/3 de su traslación alrededor del astro central (11) .
-Plutón y algunos cuerpos más pequeños se salvaron de haber sido expulsados del Sistema Solar porque coinciden en la órbita de Neptuno en 3/2 (cada 2 giros en torno al Sol de estos, Neptuno completa 3). .
. .
I): Kepler, Newton y las razones de una armonía Musical:
.
Llegamos a nuestro penúltimo epígrafe en el que tratamos muy brevemente acerca de las razones de esta “armonía celestial”, teniendo que recurrir de nuevo a Kepler y a Newton para su explicación plena (tras recordar cómo desde la más remota antigüedad se concebía equilibrio de longitud y peso directamente unidos, tal como la balanza demostraba). Siendo así repetimos de nuevo lo que decíamos en nuestro trabajos sobre temperamentos en los que ya escribí: “Su sistema de investigación parte del pitagorismo puro, deseando en un principio demostrar que los planetas en sus distancias cumplían unas leyes con arreglo a la armonía musical de esa temperación griega. Intenta con ello explicar que las distancias entre éstos se podían explicar por círculos con poliedros dentro. Elige el poliedro porque, según expone, la razón de cualquier figura dentro de un círculo (menos el de siete lados) es siempre proporcional a los intervalos musicales. Es decir que el residuo al trazar una figura dentro de la circunferencia (sea de 4, 5, 6, 8, etc. lados) es siempre un número proporcional a la Escala. Algo que ya hemos comentado al hablar de los intervalos, que aunque se resuelven en razón de 1, 2 y 3, pueden expresarse desde cualquier número del 1 al 10 (menos curiosamente desde el 7).
.
Partiendo de ello, inicia el interesante camino de intentar demostrar que igualmente las órbitas de los planetas son poliedros perfectos y que se pueden explicar sus ciclos con esa figura. Tristemente para Kepler, ve que esto es imposible, dejando de concordar entonces su teoría por la que los planetas guardaban esas distancias y formas geométricamente iguales a los intervalos de la escala musical pitagórica. Comienza, entonces (con gran pena), en otra dirección, concluyendo que estas órbitas deben de ser círculos perfectos; pero tampoco así resuelve los cálculos de un Sistema Solar en circunferencias perfectas. Ésta, que consideraba la última oportunidad para llegar a conclusiones pitagórico armónicas, se ve obligado a desecharla (...) todo ello le condujo a concluir finalmente que las órbitas de los planetas eran elípticas; con cuyas verdaderas elipses ya consigue formular las “tres leyes”, publicadas en 1609 en su Astronomía Nova .
.
De éstas, la tercera “ley armónica” dicta: “El cuadrado de los períodos de los planetas es proporcional al cubo de distancia media al Sol”. La razón que él encuentra a todo el Sistema Solar es 3/2, igual a la pitagórica, de cuyo principio procede de esta ley Tercera de Kepler, de armonía universal. Debido a que si el “cuadrado del período de giro de los planetas es proporcional al cubo de la distancia de éstos al Sol” la relación está presidida por 2 y 3, y es igual que en las razones de intervalos musicales. Recordando, asimismo, que 3/2 (y 2/3) son la razón de Quinta y Cuarta pitagórica, concluimos que la relación armónica universal del movimiento de los planetas está en base a 2, en su movimiento y a 3 en su distancia.
.
Por su parte, Newton, desarrolla su “ley de la gravedad” partiendo de la “tercera ley armónica” de Kepler, explicando con su ecuación las tres leyes del anterior astrónomo. En 1685 formula su más conocida teoría que dicta:
Fuerza = Constante [(Masa 1 x Masa 2): distancia entre ambos] dirección movimiento. Es decir, que la Fuerza es inversamente proporcional al cuadrado de las distancias.
En relación a la música y su paralelismo con la fuerza gravitatoria, concluye Newton: “Si dos cuerdas del mismo grosor están tensadas mediante pesos, sonarán al unísono cuando tales pesos estén entre sí en relación al cuadrado de las longitudes de las cuerdas. Aplicado a los cielos, los pesos de los planetas hacia el Sol guardan la misma relación que el cuadrado de sus distancias respectivas”. Ello, procede de unir las teorías de Kepler y la experimentación de Vicenzo Galilei, llegando a la conclusión de que las magnitudes y proporciones de los cielos son iguales a las de “un verdadero monocordo pitagórico”. De tal forma deduce que siendo la teoría pitagórica real, ello demostraría que Pitágoras intuía (o dedujo de algún modo) por primera vez la resolución de la gravitación y de este hecho procede la idea de la Armonía de las Esferas. Es decir, que según las conclusiones de Newton, algunos pitagóricos ya conocían los fundamentos de la gravitación y su proporción inversa al cuadrado de las distancias, relacionándola con la música donde habían observado iguales razones de intervalo (no al revés como la Historia nos narra). .
. ARRIBA: Balanza minóica de periodo Neopalacial (1500-1450 a.C.) procedente de Gournia -tal como la exhibe el Museo nacional de Creta, Heraklion, al que agradecemos nos permita divulgar su imagen-. Podemos observar la enorme precisión de esta, que seguramente se utilizaría para pesar valiosas mercancías, como las especias, o bien oro y plata -principalmente en polvo, antes de trabajarlo-. De ello no debe extrañarnos que se encuentren pesas del segundo y tercer milenio a.C. con el valor de 0,045 gramos (que correspondía al “grano” en Mesopotamia). . BAJO ESTE PÁRRAFO: Balanza estátera (o romana) de 1785 (firmada por R.0maest) y procedente de la Maestranza de Artillería de Sevilla -tal como se expone en el museo del ejército de Toledo (al que agradecemos nos permita divulgar la imagen-. Observemos la gran precisión que contendría y la posibilidad de cambiar los contrapesos para poder medir con ella grandes mercancías, tanto como otras muy pequeñas. .
. Finalmente, a todo cuanto antes hemos expuesto, hemos de unir el concepto de “resonancia”, que incorpora el “tempo” en la armonía gravitatoria. Pues una mayor masa afecta directamente a otra, cuando los cuerpos celestes comparten un número proporcional (igual o divisible por un entero) en el tiempo que transcurren sus órbitas siderales. Todo lo que explica a su vez que
no es solo el “tono” (nota o longitudes) lo que regula la armonía universal, ni el doble o el cuadrado de las distancias y masas; sino existe el número como principio de equilibrio. Un número nacido del tiempo del ritmo de giro en los planetas y que finalmente los equilibraría de un modo semejante a una escala musical, tal como ya vemos en los siguientes valores que abajo expresamos en distancias al Sol.
.
Partiendo que desde el Sol a Mercurio hay 58.000.000 de kilómetros; el lugar en el que encontraríamos un nuevo planeta, a unos 22330 millones de kilómetros del Sol, tal como vemos en las proporciones y distancias que abajo recogemos.
.
EN MILLONES DE KILÓMETROS:
DO----58.000.000 millones K. .....................SOL-MERCURIO
SI-----(58 · 2)-(58/4) = 101,5 .......................SOL-VENUS
LA----(101,5 · 2) – 58 = 145 …....................SOL-TIERRA
SOL--(145 · 2) – 58 = 232 …....................SOL-MARTE
FA----(232 · 2) – 58 = 406 …....................SOL-CERES
MI----(406 · 2) – 58 = 754 …....................SOL-JÚPITER
RE---(754 · 2) – 58 = 1450 …....................SOL-SATURNO
DO---(1450 · 2) - 58 = 2842 …....................SOL-URANO
Segunda Octava:
DO--(1450 · 2) - 58 = 2842 …........................SOL-URANO
SI----(2842 · 2)-(2842·2 : 4) = 4263 …............SOL-NEPTUNO
LA---(2842 · 2) - 58 = 5626 …..........................SOL-PLUTÓN
SOL-(5626 · 2) – 58 = 11194 ….......................SOL-SEDNA
FA—(11194 · 2) – 58 = 22330 ….................... Planeta pitagórico
.
IMAGENES, SOBRE Y BAJO ESTAS LINEAS: ARRIBA la disposición de los planetas como notas hasta Sedna. Abajo: Distancias reales al Sol y las hipotéticas. Marcado en rojo el tanto por ciento de error entre la hipótesis y la longitud real. Pese a ello, hemos de observar que las órbitas son elípticas y las muy irregulares.
.
J): En busca del planeta pitagórico:
.
Llegamos así al final de nuestro artículo en el que trataremos acerca de una de las últimas noticias que nos ha ofrecido la NASA, y que en principio protagonizaba Rodney Gomes (astrónomo del Observatorio Nacional de Brasil, en Río de Janeiro). Quien se apercibía de diversas irregularidades orbitales tras el Cinturón de Kuiper y más allá de Sedna; por lo que creía en la existencia de un planeta del tamaño de Neptuno (unas cuatro veces el tamaño de la Tierra) que orbitaría a 22500 millones de kilómetros del Sol -todo lo que encajaría con nuesta hipótesis presentada en el anterior epígrafe-. Expresando este astrónomo que podría también tratarse de un astro del tamaño de Marte, con una órbita alargada; de lo que entonces se situaría mucho más cerca.
,
Por su parte, los famosos astrónomos Brown y Batygin, observando las anomalías gravitatoria que tienen los cuerpos cercanos a Plutón y Sedna, consideran igualmente que un planeta desconocido estaría modificando sus rumbos con su atracción. Por ello aquel nuevo cuerpo tendría una masa diez veces la de la Tierra, lo que explicaría las excantricidades observadas en estos otros cuerpos celestes enanos (como Sedna, Neptuno y cinco objetos que le rodean llamados "neptunianos"). Según los cálculos suyos se trataría de un planeta desconocido con 500 veces más masa que Plutón, y el tamaño aproximado de Neptuno. Tendría diez veces máas pesado que la Tierra y su órbita sería tan excéntrica que tardaría unos quice mil años en dar una vuelta total al Sol. Este nuevo cuerpo celeste se situaría a unas doscientas veces la distancia entre el Sol y la Tierra. Como sabemos la longitud media entre nuestro planeta y el astro central es de unos 146,6 millones de Kmts; por lo que este nuevo astro se situaría hacia 25000 millones de kilómetros del Sol, con una gran excentricidad de órbita; en un punto muy cercano al que antes hemos calculado que -como podemos comprobar- era hacia 22330 mK (tal como veíamos en nuestras hipótesis).
.
Todavía no hay evidencias de su existencia, aunque los estudios matemáticos de las órbitas del cinturón de Kuiper, de Sedna o de Neptuno, dejan claro que hay un último cuerpo que los altera. Los astrónomos que más lo defienden son Konstantin Batygin y Michael Brown, del Instituto Caltech de California. Aunque curiosamente Brown fue el que más luchó hace unos ocho años por desbancar a Plutón, para que dejara de ser considerado un planeta; todo lo que hace suponer que no parten desde la teoría pitagórica que hemos desarrollado con el fin de localizar un nuevo cuerpo celeste. Pues para buscarlo conforme hemos hecho, hay que considerar a Plutón y Sedna como dos planetas. Así, después de aquellos y a unos 22.330 millones de kilómetros del Sol, se encontraría este cuerpo que Brown y Batyngin intuyen. Por su parte, otros tantos consideran que el nuevo planeta existe; entre ellos el español Pablo Santos, científico del Instituto de Astrofísica de Andalucía, quien opina que en los próximos diez años lo encontraremos. Tal como sucede con Scott Sheppard (del Instituto de Ciencia Carnegie) y Chad Trujillo (del Observatorio Gemini de Hawái), que han observado como en el cinturón de Kuiper y en el entorno de Plutón Sedna existen esas irregularidades que tan solo pueden explicarse a través de un cuerpo celeste mayor que genere el "disturbio" y las excentricidades gravitatorias que se han percibido.
.
IMAGEN ABAJO: Fotografía de los astrónomos: Michael Brown (a la izquierda) junto a Constantyn Batygin; quienes pese a haber logrado que Plutón no fuera considerado planeta, intuyen que habría un cuerpo celeste en el lugar que marcarían las leyes pitagóricas de armonía. Curiosamente, para aplicar la fórmula pitagórica que en base a “dos” calcule las distancias de los planetas desde el Sol, pudiendo justificar una armonía universal. Se precisa considerar a Sedna y a Plutón, dos planetas; tras los cuales vendría este situado a unos 25000 millones de kilómetros.
Conforme a todo lo que hemos comentado, querríamos recoger lieralmete las frases que escribí hace unos siete años en mi trabajo "Creación, temperación e improvisación" , donde decíamos: "deseamos comentar que unos ocho meses antes de pronunciar la conferencia que da origen a este trabajo, decidió la Comunidad Internacional de Astrofísicos denegar a Plutón el tratamiento de Planeta y lo degradó al de mini-planeta. Nada tenemos que objetar ni discutir sobre tal decisión, por nuestra ignorancia en astrofísica. Mas sí nos atrevemos a plantear una opinión sobre Plutón y algunos puntos acerca de la ley Bode-Titius:
.
En primer lugar, afirmar que aunque los astrónomos determinan que la presente ley no tiene base científica, en nuestra opinión hay un hecho empírico absolutamente indiscutible. Hecho que pensamos, puede fundamentarse en las leyes de armonía universal, ya conocidas desde Kepler y de ello consideramos que su progresión es igual a la de la escala musical que tanto hemos visto relacionada con el cosmos. (...) En segundo lugar deseamos añadir que, si en un futuro se encontrase un nuevo planeta a la distancia que corresponde al siguiente (tras Plutón), no solo habrían de replantarse la readmisión de este último “miniastro” entre los planetas (lugar del que ha sido destronado desde agosto de 2006), sino también a revisar los principios de esta ley. Pues uno de los motivos para considerar que la Ley de Titius-Bode no es cierta, fue la aparición de Neptuno –a medio camino entre dos (allí donde no se “esperaba”)–. Pero hemos de ponernos en el caso de qué sucedería si dentro de unos decenios (o siglos) los telescopios dejan ver un planeta a la mitad de distancia entre Plutón y el siguiente, y que posteriormente se descubriera otro en donde debe estar ese, tras Plutón (que es en el punto 772 según la Ley de Titius). Si así es, habrán de reconocer nuevamente que tal ley es exacta, pero que a grandes distancias entre planetas, en cada media longitud se sitúa otra esfera intermedia. Es decir, que no debemos descartar la idea de que antes de fin de este siglo se encontrase un nuevo planeta en el punto 772 y, a su vez, otro en el intermedio entre éste y Plutón (en el 580), y que reconozca la ciencia que dicha ley armónica se cumple perfectamente (…) Todo lo anteriormente referido nos atrevemos a afirmarlo desde nuestra ignorancia en astrofísica, y no sin pedir disculpas por no poder exponer nuestros razonamientos con argumentos más sólidos.
.
IMAGEN ABAJO: Grabado del tratado de Mitología griega y hebrea de Atanasius Kirchner. En este se representan las siete musas como los siete planetas.
.........................................................................................
CITAS:
(11): ALGUNOS DATOS SOBRE PLANETAS
Mercurio
Masa 3,302×1023 kg (0,055 Tierras)
Volumen 6,083×1010 km³ (0,056 Tierras)
Diámetro 4879,4 Km
Órbita sideral: Tarda 88 días traslación completa.
Venus
Masa 4,869 × 1024 kg (0,815 Tierras)
Diámetro 12 103,6 km
Periodo de traslación (Órbita sideral) 243,0187 días
Tierra
Período orbital sideral 365,256363004 días
Masa 5,9736×1024 kg
Volumen 1,08321×1012 km³
Marte
Período orbital sideral 686,971 días
Masa 6,4185 × 1023 kg
Volumen 1,6318 × 1011 km³
Diámetro 6794,4 km
Ceres (enano)
Período orbital sideral 1682 días
Masa 9,43±0,07 × 1020 kg2 39,47±?4
Diámetro 952,4 km
Júpiter
Júpiter es el planeta con mayor masa del Sistema Solar.
Su masa unas 2,48 veces la suma de las masas de todos los demás planetas juntos
Masa 1,899×1027 kg (no es tan denso como Tierra)
Diámetro 142.984 km
Período orbital sideral 11años 315días 1,1h
Urano
Período orbital sideral 30.799.095 días
84.323 326 años 42.718 días solares
Masa 8,686×1025 kg
Equivale a 14,5406455069 Tierras.
Volumen 6,833×1013 km³ (63,086 Tierras).
Área de superficie 8,115 6×109 km² (15.91 Tierras)
Diámetro 1.118 km
Neptuno
Período orbital sideral 60190 días (164años 288días 13h)
Período orbital sinódico 367
Masa 1,024×1026 kg4 (17,147 Tierras)
Volumen 6,254×1013 km³ (57,74 Tierras)
Diámetro 49.572 km
Plutón
Período orbital sideral (248años 197días 5,5h)
Masa 1,25 × 1022 kg1
Densidad 1750 kg/m³
Diámetro 2370 km1

![]()











¡Necesitas ser un miembro de Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae para añadir comentarios!
Participar en Arqueologia, Historia Antigua y Medieval - Terrae Antiqvae