7) LIBROS III y IV (Sobre el ritmo y el metro; Continuación del estudio sobre el Metro):

.

El tercer tomo se titula SOBRE EL RITMO Y EL METRO, y comienza del siguiente modo: “comprendo, y admito que puede darse una serie de pies, en la que está claro hasta qué número de pies se puede llegar y de ahí volver al principio." (…) “Luego ya que debe distinguirse también en el lenguaje lo que la realidad distingue, sábete que el primer género de unión es lo que los griegos llaman ritmo, y al segundo metro. Por su parte, en latín podrían denominarse numerus (número) lo uno, lo otro mensio o mensura (medida)” (...) “ritmo, metro, verso. Los tres se distinguen, de manera que todo metro es también un ritmo, no que todo ritmo sea a su vez un metro. De igual modo, que todo verso es también un metro, no que todo metro sea también un verso. Por tanto, todo verso es un ritmo y un metro. Porque, según pienso, estás viendo que se trata de algo lógico” (35) . Continuará el resto del tercer libro disertando sobre los diferentes ritmos que contienen los distintos Pies y versos, aunque en todo ello observamos un hecho musical que no contempla nunca el texto agustiniano: El Tempo. Es decir, el espíritu o velocidad con los que habrían de interpretar los pneumas (las notas). Un concepto que antaño habría resuelto gran parte de las disertaciones que les planteaban las partituras medievales. Pues aunque parece bien claro que el ritmo se marcaba en las sílabas (los Pies) y el metro en lo cada que verso dicta. Faltará para entender un texto musical escrito, la rapidez o el “espíritu” con el que deseamos lo interpreten; ya que no es lo mismo una partitura en Adagio que en Presto. Debido a ello, creemos que se extiende con tanta reticencia acerca de las formas en las que deben entenderse cada una de las fórmulas métricas. Ocupando todo ello su libro III y IV.

.

.

SOBRE ESTAS LINEAS: Una imagen de atardecer en Alcañiz, sobre la que he superpuesto el código Morse (en el cielo de y en la zona donde se halla Calanda).Como podemos observar, los principios de este sistema de comunicación llamado Morse, son semejantes a los utilizados en el cifrado de sílabas, para la métrica de versos grecolatinos. Marcando tan solo dos tipos de sonidos (corto y largo). Todo lo que produce una “melodía” muy semejante a la que contiene la música litúrgica más antigua, e incluso el canto gregoriano. Algo que a mi juicio se debió a que los cantorales medievales estaban escritos con penumas donde marcaban las notas,pero sin compases; con ritmos solo atendiendo a valor 1 y 2 (es decir: en Negras y Corcheas, o Blanca-Negra). Ello confiere al texto cantado una especie de toniquete en “morse”, del cual procederían las melopeas litúrgicas; cuyo canto se basa en notas cortas y largas. Hemos elegido la fotografía de Alcañiz, frente a las tierras de Calanda, porque en esta zona del Bajo Aragón se practican otros rituales religiosos relacionados con la música y el ritmo. En este caso con la cacofonía y la arritmia, en las famosas tamborradas de Viernes Santo; donde se toca hasta la extenuación en signo de duelo y “anarquía celeste”.

.

BAJO ESTAS LINEAS: Objetos de liturgia de Semana Santa, expuestos en la Fundación Joaquín Díaz, de Urueña (institución a la que agradecemos nos permita divulgar la imagen). Matracas y carracas que se hacían igualmente sonar durante la noche del viernes Santo; principalmente tras el “oficio de tinieblas”. Misa o Rosario, que se llevaba a cabo en el atardecer del este día, alumbrados tan solo bajo un gran candelero; del cual se iban apagando las velas conforme avanzaba la celebración o se nombraban los misterios. Al terminar el oficio, quitaban la última vela y quedaba la iglesia a oscuras; momento en el que comenzaban a sonar las matracas, carracas y tambores, en señal de duelo. Así solía permanecer en tinieblas la población entera, mientras sus habitantes agitaban estos instrumentos de percusión (en los templos, calles y casas). El significado de este rito, se relaciona con todo sonido apotropáico, que como el de los redobles y golpes de escudo, servían para ahuyentar al enemigo o al diablo. Aunque asimismo muestra el sentimiento de la música para los clérigos en el medievo; quienes interpretaban la armonía como signo celestial y la cacofonía, como símbolo infernal. Para comprender este sentido de la “acústica sagrada” (celestial o infernal) recomedamos ver este video de las tamborradas de Alcañiz y Calanda: S.Santa Alcañiz Tamborrada Ruta del tambor. Pulsar enlace:

https://www.youtube.com/watch?v=YvJnKEESuXw
.

.
.

8) LIBRO V (Estudio del Verso):

.

Es en este tomo quinto, cuando el santo realiza una exposición más matemática, acercándose a los planteamientos neoplatónicos y hablándonos del significado del número. De tal manera, nos dirá, que el “uno tiene derecho a la igualdad con todos”, razonando ese principio en algo tan sencillo como es que cualquier cifra multiplicada por 1, es igual a sí misma. Una idea que muy poco tiene “de científica”, ya que es obvio que mil unidades -o dos mil unidades- equivalen siempre a mil o a dos mil. Continuará una disertación muy limitada -en cuanto a discurso teórico- explicando nuevamente las relaciones entre cifras como 2 y 3; a la vez que su significado conforme a los múltiplos comunes (2·3=6 // 6·2=12 // 6·3=18 etc). Palabras en las que no podemos observar algoritmo o teoría cercana a las que exponían los pitagóricos; pues estos otros hablaban de los intervalos musicales, las notas y su simbolismo armónico relacionado con el Cosmos -con el fin de que veamos esa sencillez de principios expuestos por San Agustín, recojo los fragmentos que refiero del texto; para que con su lectura comprendamos lo ajenos que están al mundo de la ciencia matemática (que entre los griegos definía y razonaba números como “Pi” o “Fi”) (36) - .

.

Pasa a continuación el libro agustiniano a un planteamiento plenamente platónico, y que intitula “Armonía de los miembros en el senario: demostración geométrica”. Donde expondrá sus ideas, intentando expresarlas en base a los conceptos semejantes a los de la Sección Áurea (Fi) y al modo en que los pitágoricos realizaban sus cálculos -valiéndose de piedrecitas, a las que llamaban “cálculos” (de allí el nombre dado a la aritmética)-. Para que entendamos plenamente las ideas que explica, recogemos literalmente las palabras del texto:

.

“M: presta ahora esa atención entera, y dime si te parece que una longitud puede cortarse en cualquier número de partes.

D: toda longitud, llamada línea, tiene en sí misma una mitad y que, por ende, se la puede dividir perpendicularmente en dos: y como esas mismas dos líneas, que nacen de tal división, son sin duda líneas, es manifiesto que también en ellas se puede hacer otro tanto. En consecuencia, también una longitud, por pequeña que sea, se puede dividir en cuantas partes se quiera.

M.: Rapidísima y verísima respuesta. Pues mira ahora esta otra cuestión: si con seguridad podría afirmarse que toda longitud, desarrollada en superficie igual a la línea de la que nace, es equivalente a su cuadrado. Porque si la superficie se extiende menos o más que mide en longitud la línea desde la cual se extiende, no resulta un cuadrado. Si lo hace de modo equivalente, no hay otra cosa que un cuadrado.

D.: Comprendo y estoy de acuerdo. Pues ¿qué hay más exacto?

M.: Por tanto, estás viendo ya su consecuencia, pienso yo: si en el lugar de la línea se ponen una tras otra en fila, a todo lo largo, piedrecitas iguales, esta longitud no llegaría a la forma de cuadrado a no ser que las piedrecitas se hayan multiplicado por el mismo número. Como si, por ejemplo, pones dos piedrecitas, no harás un cuadrado sino poniendo otras dos a lo ancho; si pones tres a lo largo, han de añadirse seis, pero distribuidas en forma de dos grupos de tres, igualmente a lo ancho, pues si se añaden a lo largo, no resulta una figura geométrica. Porque la longitud sin la anchura no es una figura. Y así proporcionalmente se pueden considerar todos los números. Pues igual que 2 X 2 y 3 X 3 forman un cuadrado numérico, así 4 X 4, 5 X 5, 6 X 6 y los demás números hasta el infinito” (37) .

.

.

IMAGEN ARRIBA : Una fotografía mía en la que marco las proporciones de la Sección áurea, tal como se describe ya en Euclides y como la define Pacioli en el Renacimiento:

A_______________B_____________________C

(linea con tres secciones que son):

_______________AB

______________________________________AC

______________________BC

Cuando la distancia de A a C, dividida entre la que hay entre B a C; es igual a la longitud de B a C,dividida por la que hay de A a B. Es decir: AC / BC = BC / AB

Este hecho no se da entre 1, 2, 3 como parecen indicar Platón y San Agustín; sinó que es algo que existe en cifras proporcionales a "FI"=1,6180339887....

Es decir cuando AC/BC = BC/AB = 1,681...= F

.

IMAGEN ABAJO: Forma en que los pitagóricos explicaban la aritmética; usando cálculos (pequeñas piedras, de las que se servían para hacer ábacos o para conformarlas en lineas, cuadrados y cubos). Como vemos en el ejemplo, se observan claramente las tres dimensiones: PRIMERA DIMENSIÓN -LINEAL- (Dos); SEGUNDA DIMENSIÓN -PLANO- (Dos al cuadrado =4); TERCERA DIMENSIÓN -REAL- (Dos al cubo = 8).

.

.

En las imágenes anteriores hemos resumida la exposición lineal de “FI”, así como el modo en que los pitagóricos explicaban sus números (lineales, cuadrados, cubos). Si releemos el texto recogido antes de ellas, veremos que el santo se refiere a algo similar; aunque la explicación que nos da es muy limitada. Sin relación con la sección áurea o con la progresión numérica y geométrica, conforme las dimensiones. Simplemente realizando una exposición muy breve, pero que demuestra como San Agustín conoció el método de enseñanza de los pitagóricos, que explicaban la matemática valiéndose de estos cálculos. Tras lo recogido, el santo desea elevar sus ideas al ámbito temporal (es decir, pasar del Espacio al Tiempo), para lo que escribe:

.

“M.: Piensa ahora si existe una longitud de tiempo.

D.: ¿Quién habrá dudado de que no existe tiempo sin alguna longitud?

M.: Pues bien: ¿no puede ocupar el verso una cierta longitud de tiempo?

D.: Hasta es necesario que lo tenga.

M.: ¿Qué cosa mejor ponemos nosotros en aquella longitud en lugar de las piedrecitas? ¿Los pies que necesariamente se dividen en dos partes, o sea, en arsis y tesis, o más bien los semipiés que ocupan cada arsis y tesis?

D.: Juzgo que los semipiés sustituirán más adecuadamente las piedrecitas.

(Exposición de la maravillosa armonía del senario)

M.: Bien, ¿pueden siete semipiés por sí mismos formar un verso completo?

D.: Claro que pueden, porque el primer verso tiene tantos semipiés como el verso más corto, añadiendo al final un silencio.

M.: Exactamente dicho. Mas para que pueda ser verso, ¿cómo se divide en dos miembros?

D.: Así: en cuatro y en tres semipiés.

M.: Por tanto, eleva al cuadrado cada una de sus partes y observa cuántas hacen 4x4.

D.:16.

M.: ¿Y 3x3?

D.: 9.

M.: ¿Y todo en conjunto?

D.: 25.

M.: Luego como siete semipiés pueden comprender dos miembros o hemistiquios, elevados cada uno de ellos al cuadrado, hacen la suma total de 25. Y es una parte del verso heroico” (38) .

.

La última idea, creemos que se corresponde a una identificación entre el triángulo perfecto y el poema perfecto. Describiendo san Agustín los números 3, 4, 5, 16 y 25 como claves de su metrología; todo lo que se uniría quizás con aquel equilátero perfecto: El triángulo de 3, 4 y 5 (cateto a=3 // cateto b=4 // hipotenusa=5). Por su parte, a mi juicio este párrafo anterior es la clave de “Sobre la Música”; donde el autor desea expresar su idea, consistente en que si sabemos que existe un “valor Espacio” en la música, medido por un número y que se refiere a las distancias de los intervalos (en base a la longitud de la cuerda que vibra, el peso del martillo que se golpea o el diámetro de una placa que se bate). Ha de existir también un “valor Tiempo” tan solo descrito por el ritmo. Hecho este que le posibilita al maestro (San Agustín) a realizar una reforma del pitagorismo, escribiendo su libro en el que tratará solo de este segundo parámetro que contiene la música: El Tiempo. Un tempo que mide rítmicamente en Pies de verso; todo lo que complica enormemente su teoría, pues siquiera en la época tenían medios para delimitar el ritmo, ni escribir los compases. Debiendo acudir el santo a la métrica de la poesía, para explicar EL TIEMPO en la música.

.

Una idea que por muy creativa que nos pudiera parecer, no tiene sentido frente al principio del mundo pitagórico, que se basa en las distancias existentes entre las notas (los intervalos) y no en el ritmo de aquellas. Pues esta filosofía no concibe la acústica sin física, por cuanto la música es en si mismo, sonido y tempo (a la vez).Unas ideas que a mi juicio, sin duda proceden de los templos mesopotámicos y egipcios; donde existía un gremio sacerdotal dedicado precisamente a la afinación y creación de instrumentos musicales. Arpas, liras o flautas; que no solo habían de fabricar conforme a una escala común; sino que además debían mantener y lograr afinar. De tal manera, es sabido que en los templos del Nilo se alquilaban estos instrumentos; estando multado devolver liras, arpas o panduras, con las cuerdas rotas o desafinadas. Debiendo pagar una cuota por ajustarlas y arreglarlas, todo aquel que hiciera uso de estos enseres musicales (alquilados para fiestas, celebraciones o funerales).

.

Desde las mencionadas teorías para la afinación y construcción de instrumentos, nació a mi juicio el pitagorismo; un arte que de seguro estudió el maestro samio cuando vivió en un templo de Tebas (la actual Luxor) y en Babilonia (donde se supone que fue raptado por Cambises, cuando este general llamado el brujo, invade el sur del Nilo). De aquí procederían esos conocimientos que mezclaban religión y arte; basados en la astronomía, las Escalas y la ciencia de hallar las notas.Entendiéndose así por qué los profesores Luque y López Eisman escriben la introducción a su edición del texto agustiniano que: “En el siglo I Filón de Alejandría habla de los conocimientos astronómicos y de las prácticas y creencias de los astrólogos caldeos: `Ellos -dice- han sabido ensamblar (armonizar) las cosas que hay en la tierra con las que están arriba; las cosas del cielo con las de la superficie y han mostrado como la base de proporciones de la música tiene lugar con las más melodiosas consonancias en el Universo. En virtud de la comunidad y simpatía de las partes, unas con otras. Que aunque separadas en diferentes formas y lugares, no tienen naturaleza distinta, ni morada diferente; dado su parentesco´" (39) .

.

.

IMAGEN ARRIBA: De nuevo expongo un diagrama de las distancias de los intervalos, temperados a en formas pitagóricas y en la actual (utilizando la cuerda sexta de la guitarra como Monocordo). A la izquierda, las notas. En la columna primera, la afinación conforme Pitágoras y sus discípulos explicaban. En la segunda, la Enharmónica; temple que se considera originado por la escuela de Lesbos y más concretamente por el músico Terpandro. A la derecha, la afinación que hoy utilizamos, denominada “Igual Templada”, descendiente de la que se inició en tiempos de Bach, llamada por entonces “bien temperada”. El gráfico es de un trabajo mío presentado hace años en la Fundación Joaquín Díaz (40) .

.

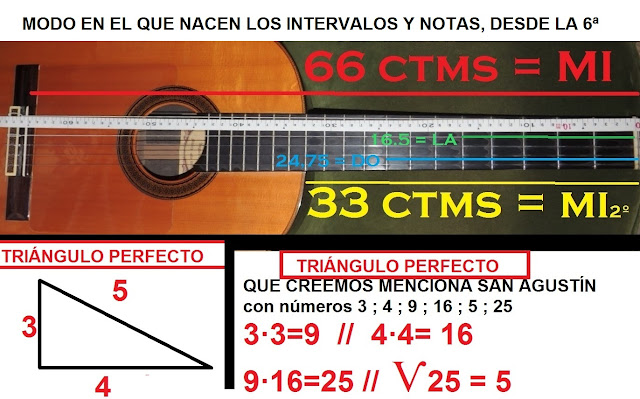
IMÁGENES, ABAJO: Primeramente, ejemplo sobre la guitarra, usando como monocordo la sexta cuerda. De nuevo reproduzco esta fotografía, para que todos comprendamos el modo en el que surgen las notas por el procedimiento pitagórico: Dividendo primero la cuerda entera en dos partes, sabiendo que entre ambos puntos están el DO1 y el DO2. Luego se irá multiplicando por 4/3 o por 2/3, repetidamente (hasta encontrar las doce notas).

Mas abajo y en la misma imagen: El triángulo perfecto (3,4,5) que creemos refiere San Agustín al hablar de la relación numérica entre: 3, 4, 5, 9, 16 y 25. ROGAMOS DISCULPAS, PUES ESTE DIBUJO CONTIENE UN ERRATA, NO ES 9·16=25; SINO 9+16=25.

.

.

Los textos agustinianos que hemos recogido anteriormente, son de un claro tinte platónico, aunque no podemos clasificarlos de pitagóricos debido a la simplicidad de sus planteamientos matemáticos. Coincidiendo en muchos de los parámetros que explica el pitagorismo, tiene como diferencia con ellos, la sencillez de las teorías presentadas y el hecho de querer equiparar la armonía solo al ritmo (no al sonido).Pero no solo eso, sino que además, trata la medición del tempo musical como algo derivado de la gramática y de la métrica poética; todo lo que desvirtúa la posibilidad de entender como teoría bien estructurada, la que nos expone -al menos, científicamente hablando-. Para que comprender mejor cuanto digo, vamos a recoger algunos puntos de conexión entre el pitagorismo y el texto que analizamos; cuyas bases más cercanas podrían ser las siguientes (en referencia al significado del número):

PARA EL PITAGORISMO tal como ya expuse (41) :
.

-El 1, que significaba la “mónada” o unidad creadora,

-El 2 o diada, símbolo de la diversidad, de la dualidad y lo femenino

-El 3 o tríada= monada+diada. Simbolo del hijo, la armonía, el tiempo. Unido por tres puntos. geometricamente es el plano, la segunda dimensión, con su comienzo en el triángulo.

-El 4 era la dualidad de la diada = 2 x 2 y 2+2. La ley universal inexorable, clave de la Naturaleza y la justicia.

-El 5 era el número sagrado raiz del 10, la representación de dios. Significaba el matrimonio, muy posiblemente por ser el número de dedos. 
.

PERO DE FORMA MUY DIFERENTE, LOS PITAGÓRICOS NOS HABLAN DE ALGORITMOS COMO EL SIGUIENTE QUE RECOJO, PARA CALCULAR Y CONOCER SU TEORÍA DE LA ARMONÍA:

La afinación pitagórica se expresa:

Quinta (elevada al número de quintas) dividida por Octava elevada a número de octavas

Q* / O** (siendo * el número de quintas // y ** el número de octavas)

= 3/2 * : 2 **

Lo que equivale a:

A= (a+b)/2 1/H = 1/2 (1/a + 1/b) ; G/a = b/G

Verificándose que a/A = H/b ; G/A = H/G

Produciendo

el DIATESSARON= 3/4 (1/Cuarta)

el DIAPENTE = 2/3 (1/Quinta)

el DIAPASON = 1/2 (1/Octava)

.

Evidentemente, en el texto agustiniano no vemos nada referente a este tipo de teoremas o principios; sino todo él nos habla de rimas y de métrica en la poesía. Algo que se explicaría debido a que el santo era un afamado grámatico (conocido como tal desde su juventud y antes de convertirse). Pudiendo haber intentado el santo crear una nueva teoría de la armonía en base a la medida y no al sonido de las notas. Ideas que quizás si las hubiese unido a los ciclos de los planetas (sínodos en que giraban o movimientos anuales, mensuales y diarios) quizás sí hubieran tenido un concepto más pitagórico. Aunando el tiempo del Universo, con los tempos de la música. Pero el modo en que nos presenta su teoría; intentando una armonía en base a 1/2, 2/3 y3/4 (Octava, Quinta y Cuarta), en razón a las sílabas de los versos. Creemos no tiene explicación plenamente lógica; habida cuenta que estas relaciones nacen de proporciones entre 1 y 2, por efecto de la pronunciación de palabras. Sin nada que ver con los paralelismos de los intervalos musicales; que son hechos físicos y no simples ideas sobre el número. Es decir; que la armonía pitagórica no es una teoría, es un hecho acústico y espacial mostrable y demostrable. Tanto que de ella procede nuestro actual sistema de afinación. Otra cosa es ya su plasmación o idealización sobre el Cosmos, donde los pitagóricos ven aquella armonía, reflejada en los astros.Ideas que siguieron personajes como  Galilei, Kepler y Newton; para resolver sus leyes y paradigmas -aunque a día de hoy no pueda tenerse como una teoría del Universo, demostrada-. Por cuanto expreso, si el santo hubiera llevado aquellas leyes del tempo en la música (o de la rima) sobre los ciclos de giro de la Luna, Marte, Venus etc.; ciertamente nos encontraríamos ante un texto pitagórico. Aunque tal como lo leemos, tan solo puedo describirlo como “platónico” y muy básico de planteamientos.

.

IMAGEN ABAJO: Esquema mío con las diferentes funciones de la Tetratkis, el principio activo de los pitagóricos. Esta figura “sagrada” para los discípulos del samio, consistía en una pirámide construida con cálculos, en la que arriba tenía uno; en la siguiente fila, dos; en la tercera, tres; y en la última, cuatro piedrecitas. En el Tetratkis se encontraba en primer lugar todas las proporciones de la armonía musical; tal como podemos ver en mi dibujo, en el que se observa que cada fila dividida por la de abajo, produce las fracciones correspondientes a 1/2 ; 2/3 y 3/4 . Por su parte, la suma total de los cálculos usados es diez (1+2+3+4+5). Algunos autores, como Guillermo L. Correa (42) , ven en partes del texto agustiniano referencias a la Tetratkis, habida cuenta que el santo menciona repetidamente los números 1, 2, 3 y 4; afirmando que la base diez es la perfecta y que el 10 es uno de los números sagrados. Aunque yo -personalmente- no veo en Sobre la Música una clara referencia a la Tetratkis, sino simplemente a la base decimal de cálculo (que recordemos era de origen egipcia y milenaria, pues en tiempos de las pirámides los súbditos del faraón ya escribían sus cifras como: 1, 10, 100, 1000 etc). Por lo demás, resulta normal que el santo no mencione esta tetratkis, porque era el eje del dogma pitagórico; sobre el que juraban sus discípulos. Debiendo prometer fidelidad absoluta a ella, tal como el católico lo hace con la fe en Cristo (todo lo que explicaría la ausencia de la palabra e ideas sobre la Tetratkis en el texto que analizamos).

.

.
.

9) LIBRO VI: Dios, Fuente y lugar de los números eternos

.

El tomo último trata acerca de la mística del número; siendo este libro el que más podemos considerar neoplatónico. Comienza con un capítulo que titula “Dios, Fuente y lugar de los números eternos”; desarrollando luego una primera parte en la que trata de “Las armonías de las almas y sus grados, o de Los ritmos del alma”. Ideas con las que claramente desea unir la teoría de la Armonía Universal a otras sobre el espíritu, de raíz cristiana. Los distintos epígrafes de la segunda parte (de este libro VI), manifiestan una igual intención; tal como podemos ver en sus intitulaciones: “Dios, fuente de las armonías eternas; Sección primera: Las armonías eternas; Primera proposición: Existencia racional de la armonía eterna; Tercera proposición: Por la caridad a Dios y a las armonías eternas; Conclusión: El alma, guía del cuerpo por las virtudes cardinales”. Observándose que se trata ya de un texto místico, en que se desea unir la teoría del número a las enseñanzas cristianas.

.

Finalmente, concluye la obra con un epílogo en el que expresa de nuevo sus ideas sobre la Trinidad. Comenzando este final con frases que aluden a sus pequeños conocimientos del tema musical. Para terminar diciendo que cuanto escribe tiene como función refutar las teorías de los herejes, todo lo que expresa de la siguiente forma:

.
M.: “De tema tan grande, tan poquito como soy, he discutido contigo lo que pude y como pude. Mas si algunos lectores vienen a tener a mano nuestra conversación, ahora consignada por escrito, sepan que todo esto ha sido redactado para espíritus mucho más débiles que los de aquellos que, siguiendo la autoridad de los dos Testamentos, honran a la consustancial e inmutable Trinidad del Dios único y sumo, de quien todo proviene, por quien todo es, en quien todo subsiste, y a Ella rinden culto por la fe, la esperanza y la caridad. Porque éstos están purificados no por la centella de los razonamientos humanos, sino por el fuego poderosísimo y ardentísimo de la caridad.

Nosotros, por nuestra parte, mientras juzgamos que no deben olvidarse aquellos a quienes los herejes seducen con la falsa promesa de su razón y de su ciencia, hemos avanzado con mayor lentitud, en el estudio de estos caminos, que aquellos santos varones que, volando sobre estas rutas, no creen merezca la pena atender a ellas. Sin embargo, nosotros no nos atreveríamos a hacerlo si no viésemos que muchos hijos piadosos de la Iglesia católica, nuestra bonísima Madre, después de haber adquirido en sus estudios de juventud la capacidad suficiente para hablar y discutir, han hecho esto mismo por la necesidad de refutar a los herejes” (43) .

.

Conclusión:

En ese último párrafo se advierte la intención del santo de sincretizar el pitagorismo con el cristianismo. Algo que claramente se entiende cuando leemos:"no deben olvidarse aquellos a quienes los herejes seducen con la falsa promesa de su razón y de su ciencia, hemos avanzado (...) en el estudio de estos caminos, que aquellos (...) no creen merezca la pena atender (...) no nos atreveríamos a hacerlo si no viésemos que muchos hijos piadosos de la Iglesia católica (...) después de haber adquirido en sus estudios de juventud (...) han hecho esto mismo por la necesidad de refutar a los herejes". Todo lo que explica y deja clara la intención de San Agustín. Quien tras haber estudiado multitud de escuelas filosóficas -durante su juventud-; desea sincretizar partes de este saber clásico que domina, con el fin de que los “herejes” no se lleven a muchos otros hacia su campo -valiéndose de unos mayores conocimientos-. Consecuentemente y en base a sus posibilidades (como gran gramático); a mi juicio, creó el santo esta nueva teoría de la armonía, basándose en la poesía. Al ser un conocido especialista en poética pudo idear este sistema; pero probablemente también por desconocer muchos de los pormenores del mundo musical y matemático. Todo lo que le llevaría a expresar los paradigmas pitagóricos de manera muy simple y basándose en algoritmos como el que continuamente refiere (que la unión de 1, 2 y 3; se halla en la razón de que 3=2+1). Unos teoremas, que demostrarían como seguramente no dominaba la base numérica, ni física, del pitagorismo. Resolviendo sus teorías matemáticas con simples relaciones de sumas, multiplicaciones, divisiones y restas. Todo lo que se comprende, porque el pitagorismo inicialmente era de tal complejidad, que en la época en que se escribió la obra agustiniana analizada, ya se habrían perdido gran parte de sus secretos y principios.

.

BAJO ESTAS LINEAS: Convento de Los Trinitarios (fundado en Madrid en 1608), donde se mandó enterrar Miguel de Cervantes, debido al cariño que guardaba a estos monjes. El autor de El Quijote, permaneció cinco años apresado en Argel (junto a su hermano Rodrigo) y gracias a los Trinitarios fue rescatado de aquel terrible cautiverio. El clérigo Juan Gil (nacido en Arévalo y nombrado Redentor General de Castilla), inició el proceso para el pago del rescate y la liberación de ciento ochenta esclavos, entre los que se encontraba Miguel y su hermano. Una operación de gran riesgo, que lograron culminar en 1580; tras haber recaudado enormes sumas de dinero, logrando llegar con las cajas de caudales hasta Argel -donde fueron comprando la “vida” de los allí retenidos-. Como si de un destino extraño se tratase, al igual que el cristianismo entró en la Península desde Argelia; en esta tierra realizaron los monjes hispanos algunas de las labores más prodigiosas. Principalmente los trinitarios, quienes llegaban a cambiarse por los prisioneros españoles que habían vendido como esclavos los pitaras berberiscos. Juan Gil (que salvó a Cervantes y a su hermano de la esclavitud) fue inicialmente un teólogo especializado en lógica y artes; profesor en Salamanca, donde enseñaba la obra de San Agustín. Finalmente, parece que se vio atraído por conocer la tierra que engendró aquel santo, llegando a ir hasta Argelia a rescatar cautivos.

.

..............................................

CITAS:

...............................................

(35): Introducción: Qué es ritmo, metro y verso. Diferencia entre ritmo y metro 1 1.

(36): SOBRE LA MÚSICA (traducción, ALFONSO ORTEGA) LIBRO V; ESTUDIO DEL VERSO

El nombre del verso 1 1.

Razón profundísima de la reducción de la desigualdada La igualdad entre los semipiés 7 (13).

El número 1 tiene el derecho de igualdad con los otros

Efectivamente, te pregunto yo ahora: cuando digo 2 y 3, ¿cuántos números estoy diciendo?

D.: Dos, es cosa sabida.

M.: Por tanto, 2 es un número, tanto como lo es el 3; y así cualquier otro que digamos.

D.: Así es.

M.: ¿No te parece, por ende, que el 1, sin cometer absurdo, se puede comparar con cualquier otro número? Si no podemos decir que 1 sea 2, afirmarse puede sin error que 2 es de alguna manera 1, e igualmente que 3 y 4 son 1.

D.: Lo admito.

M.: Oye esto otro: dime cuántos son 2 por 3.

D.: Seis.

M.: ¿Y hacen lo mismo 6 y 3?

D.: De ninguna manera.

M.: Ahora quiero que multipliques 3 por 4 y me das el total.

D.: Doce.

M.: Estás viendo asimismo que 12 son más que 4.

D.: Y mucho, por cierto.

M.: Para no insistir ya más, hay que establecer una regla como ésta: a partir de dos y, sucesivamente, cualquiera que sea el número que tomes, el menor multiplicado por el mayor debe necesariamente sobrepasar a este último.

D.: ¿Quién lo habrá dudado? Porque ¿qué número es en plural menor que el 2? Con todo eso, si lo multiplico por 1.000, superará 1.000 hasta formar el doble.

M.: Es verdad lo que dices. Pero toma el 1, y después cualquier otro mayor, y como hemos hecho en los anteriores, multiplica el mayor por el menor. ¿Superará igual que antes al mayor?

D.: No, por cierto, sino que el menor será igual al mayor. En efecto: 2 x 1 = 2; 10 x 1 = 10; 1.000 x 1 = 1.000; y por cualquier número que lo multiplicare, el 1 debe quedar igual.

M.: —Por tanto, el número 1 tiene un cierto derecho de igualdad con todos los demás; no sólo porque es un número, sino también porque multiplicado tantas veces por el otro da siempre lo mismo.

(37): SOBRE LA MÚSICA (traducción, ALFONSO ORTEGA) LIBRO V

Armonía de los miembros en el senario: demostración geométrica 12 (25).

(38): Idem cita (37)

(39): Filón Migr. 178 -cita tomada de pag 18- ; SOBRE LA MÚSICA seis libros // Introducción, traducción y notas JESÚS LUQUE MORENO Y ANTONIO LÓPEZ EISMAN //ed. Gredos Madrid 2007

(40): Angel Gómez-Morán Sanfafé: Creación, temperación e improvisación en SIMPOSIO SOBRE PATRIMONIO INMATERIAL; LA VOZ Y LA IMPROVISACIÓN Fundación Joaquín Díaz Valladolid 2008.

(41): Idem cita (40)

(42): Op. Cita (4) Guillermo L. Correa Pabón.

3.7. LA TETRACTÝS (pags 93 y ss)

(43): SOBRE LA MÚSICA (traducción, ALFONSO ORTEGA) LIBRO VI; Conclusión de la obra-59